日本応用数理学会
2018年 年会
プログラム
2018年9月5日
9月3日
9月4日
9月5日
▷ 総合講演1 [9月4日:15:00-16:00:豊田講堂]
- ゼータ関数の普遍性について / 松本 耕二(名古屋大学)
▷ 総合講演2 [9月4日:16:10-17:21:豊田講堂]
- 応用数理としての風が吹けば桶屋が儲かる / 菊池 昇(豊田中央研究所)
▷ [研究部会 OS] ウェーブレット(1) [9月3日:15:00-16:20:C]
- [OS特別講演:40分] On the Double Windowed Ridgelet Transform and its Inverse / 木下 保 (筑波大学 数理物質系), ○藤井 克哉 (筑波大学 数理物質科学研究科) [概要]
リッジレット変換は、ラドン変換と1次元ウェーブレット変換を合成して得られる変換であり、今日ではニューラルネットワークに関連した人工知能の分野などでも応用されている。今回、我々はラドン変換を窓ラドン変換に置き換え、2つの窓に関するリッジレット変換を新たに提案する。本講演では、その再生公式や性質などを考察したい。
- 信号の周波数ピークごとの分解と瞬時周波数 / ○山内 佑維 (大阪教育大学) [概要]
FFTでは時間幅の逆数より細かく周波数を見ることができないが, 例えば楽譜において半音の基本周波数の差が音の長さの逆数より細かいということがあった. この場合でも音名を特定したい為まず簡単な信号から瞬時周波数を求めた. 無変化の純音の瞬時周波数, 複数の純音を含む信号の周波数成分ピークごとの各瞬時周波数, 雑音入り信号の閾値以下の周波数を無視した場合の瞬時周波数を調べた.
- 画像分離問題における回転角度と平行移動量の同定について / ○守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学), 萬代 武史 (大阪電気通信大学) [概要]
元画像を回転・平行移動した画像の重み付き重ね合わせを観測し,複数の観測画像から元画像を分離する問題を考えたい.
本講演では,複数の観測画像から,元画像の枚数,相対的回転角度と相対平行移動量を推定するための方法について考察する.
▷ [研究部会 OS] ウェーブレット(2) [9月3日:16:30-17:30:C]
- [OS特別講演:40分] ウェーブレット解析による聴性定常反応波形高速加算法の検証 / ○井川 信子 (流通経済大学), 守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学) [概要]
Galambosらによる40 Hz event related potential (40 Hz ERP) に関する報告を応用して,聴性定常反応波形の高速加算処理法を提案している.ウェーブレット解析を用いて,その妥当性と有効性の比較検証を試みた結果について報告する.
- 両側四元数フーリエ変換と右側四元数フーリエ変換に関するいくつかの注意 / ○芦野 隆一 (大阪教育大学) [概要]
四元数は非可換なため,四元数値関数のフーリエ変換の定義にはいくつかの流儀がある.
採用するフーリエ変換の定義に応じて,成立する性質が異なる.
この講演では,両側四元数フーリエ変換と右側四元数フーリエ変換を紹介し,
いくつかの成立する性質の違いについて説明する.
▷ [研究部会 OS] 応用カオス(1) [9月3日:09:30-10:50:A](座長:山口 明宏(福岡工業大学))
- ベイズ理論によって捉えるカオス性と情報量との間の一般的な関係式について / ○梅野 健 (京都大学大学院情報学研究科数理工学専攻) [概要]
混合性を持つカオス(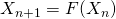 )の確率時間発展則は、ペロン=フローベニウス方程式(以下PF方程式と略す。確率が、力学発展の前後で保存することを表現する式)で書け、
)の確率時間発展則は、ペロン=フローベニウス方程式(以下PF方程式と略す。確率が、力学発展の前後で保存することを表現する式)で書け、 で、不変測度
で、不変測度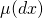 に収束する。著者は、最近、このカオスのPF方程式が、カオス力学系
に収束する。著者は、最近、このカオスのPF方程式が、カオス力学系 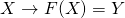 によってデータ
によってデータ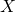 が
が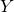 に変換される場合、出力結果としてのデータ
に変換される場合、出力結果としてのデータ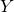 を得た時に、事前のデータが
を得た時に、事前のデータが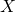 であった時の事後確率
であった時の事後確率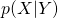 を事前確率
を事前確率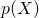 から与えるベイズの定理の確率の変換を与える式に他ならないことを発見した。この場合、事後確率の計算に必要な尤度が、PF方程式から
から与えるベイズの定理の確率の変換を与える式に他ならないことを発見した。この場合、事後確率の計算に必要な尤度が、PF方程式から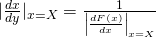 で計算できることになる。
この尤度と事前確率との積が観測結果が
で計算できることになる。
この尤度と事前確率との積が観測結果が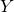 となる確率の寄与分であり, 事後確率
となる確率の寄与分であり, 事後確率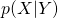 が計算できる。
そこから、事前確率が力学系の不変測度に等しい時、カオスの発展則によって確率が不変となるので、カオスの時間発展則に基づき繰り返し推論していく場合、次の時刻での力学反転においても、事前確率の不変性を保つと言う優れた性質を持つ。本講演では、これらのカオスの確率発展則とベイズ理論的な解釈によって、ベイズの逆確率のエントロピー
が計算できる。
そこから、事前確率が力学系の不変測度に等しい時、カオスの発展則によって確率が不変となるので、カオスの時間発展則に基づき繰り返し推論していく場合、次の時刻での力学反転においても、事前確率の不変性を保つと言う優れた性質を持つ。本講演では、これらのカオスの確率発展則とベイズ理論的な解釈によって、ベイズの逆確率のエントロピー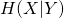 に関して一般的に
に関して一般的に![Rendered by QuickLaTeX.com H[X|Y]=\Lambda[Y]+D(q\|p)](https://annual2018.jsiam.org/wp-content/ql-cache/quicklatex.com-b54913e86f4f1a0cd15f00a53c20530e_l3.png) が成立し、一般にデータのリアプノフ指数
が成立し、一般にデータのリアプノフ指数![Rendered by QuickLaTeX.com \Lambda[Y]](https://annual2018.jsiam.org/wp-content/ql-cache/quicklatex.com-849edd12cfb73c33d8e4d418748c9dbc_l3.png) 以上であることを示す。事前分布が不変測度に一致する時にそれが, KSエントロピーとリアプノフ指数に等号で成立する(Pesinの等式)に一致することを示す. この様に, 本理論では,
頻度論(エルゴード理論)とベイズ推論がうまく両立可能であるとともに、ベイズ理論によって、データの持つカオス性を捉え直すことができることを示す。
以上であることを示す。事前分布が不変測度に一致する時にそれが, KSエントロピーとリアプノフ指数に等号で成立する(Pesinの等式)に一致することを示す. この様に, 本理論では,
頻度論(エルゴード理論)とベイズ推論がうまく両立可能であるとともに、ベイズ理論によって、データの持つカオス性を捉え直すことができることを示す。
- カオス尺度のカオス判定力向上に向けた試み / ○井上 啓 (山陽小野田市立山口東京理科大学) [概要]
カオス尺度は情報理論の観点から導入されたカオスを定量化する指標であり、力学系に関する情報が時系列しか得られない場合でも計算可能といった利点がある。しかし、実際のカオス尺度の計算では、入力分布と出力分布の分割の切れ目が異なること、2次元以上の系では出力分布と入力分布の直交系が異なること、が考慮されていないといった点に改善の余地がある。そこで、これらの分割の切れ目や直交化の影響を軽減するために、カオス尺度の改良を試みる。
- 1次元カオス写像におけるカオス尺度の極限値に関する考察 / ○奥富 秀俊 (東芝情報システム株式会社), 真尾 朋行 (東芝情報システム株式会社) [概要]
カオス尺度と呼ばれる指標はリアプノフ指数とよく似た挙動を示すことが知られている.発表者らは先行研究において両者の数理的関係性を解析的に示した.そこで両者の差分量が興味の対象となる.本発表では,代表的な1次元カオス写像を対象として,両者の差分を与える関数とその評価についてに考察する.
- カオス尺度の計算方法について / ○真尾 朋行 (京都大学/東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学) [概要]
生体データ等の分析において,データのカオス性に着目した分析法としてカオス尺度を用いることを検討している.カオス尺度は,カオスを定量化する指標として提案されている.本発表では,KSエントロピーやリアプノフ指数との関係を考慮しながら,カオス尺度の計算方法について考察する.
▷ [研究部会 OS] 応用カオス(2) [9月3日:11:00-12:20:A](座長:井上 啓(山陽小野田市立山口東京理科大学))
- APFAのカオス性 / ○中澤 勇夫 (京都大学), 梅野 健 (京都大学) [概要]
情報通信の爆発の時代を迎えて、移動通信システムに於いても高速・大容量化、超多数端末接続、超低遅延、超高信頼性を目指した第5世代移動通信システム「5G」の2020年の実用化を目標に研究開発、標準化が進められている。
カオス理論の研究ではパワー一定カオス拡散符号の1種であるAlmost Periodic Function Codesを用いた拡散符号を周波数軸に移した概周期周波数配置(Almost Periodic Frequency Allocation,APFA)の通信分野への適用の研究を進め、5G要求条件に沿った100万チャネル以上の超多重化を可能とする通信方式を提案し,その実現性を明らかにしている。
本研究では非周期性を持つAPFA通信方式は同期系のOFDM方式とガウス雑音の中間に位置することを説明するもので、同期系のOFDM通信方式、ランダム雑音であるガウス雑音、カオス符号等の各々の分野の評価を横並びで比較してAPFAのカオス性を相互検証する。
- 2016年台湾地震の電離層における先行現象 / ○後藤 振一郎 (京都大学), 打田 凌馬 (京都大学), 五十嵐 喜良 (京都大学), Chen Chia-Hung (成功大学), 梅野 健 (京都大学) [概要]
規模が大きな地震に関して、地震前に電離層で何らかの意味で異常が起こることが知られている。しかし、そのメカニズムや異常が発生するかどうかのマグニチュードしきい値に関して解明すべき課題は多い。一般的な議論は現段階では難しいので、まずはどのような条件や手法でこの種の先行現象が観測されるか、様々な解析例を集めることが上述の課題を解決する手がかりになるであろう。一方、2016年2月5日に台湾南部でモーメントマグニチュード6.4の内陸型地震が発生した。この地震の先行現象として電離層での異常現象をIwata-Umeno の方法で捉えることができたので、報告する。
- Arnoldの猫写像のカオス真軌道の生成と乱数性の解析 / 多久島 秀平 (福岡工業大学), ○田村 健太郎 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学), 山口 明宏 (福岡工業大学) [概要]
代表的なカオス写像の一つとしてArnoldの猫写像が知られており,擬似乱数生成器に応用されている.Arnoldの猫写像について有限精度の数値計算によって生成された軌道と,無限精度の計算のもとでの真の軌道との同等性は自明ではない.本研究では,代数的数を用いて生成した無限精度のカオス真軌道と有限精度の計算で生成した軌道について,乱数性の比較を行う.更に,Arnoldの猫写像で生成した系列は相関を有しているが,生成される2値系列について過去の状態とのXOR演算を行うことで乱数性が向上することを数値実験によって示す.
- 力学系の混合性の電磁気学への応用 / ○杉本 哲 (京都大学工学部情報学科), 梅野 健 (京都大学情報学研究科数理工学専攻) [概要]
直交関数系のLebesugue スペクトルとして性質がよく知られているのはChebyshev 多項式程度であったが、
今回の研究発表会では、Legendre 多項式の系列が混合性を持つことを証明する。
Legendre 多項式の性質を理解することは、電磁気学など物理学で登場する微分方程式の解として頻繁に登場するので重要である。
今回はLegendre 多項式が登場する一例として、電磁気学において行われる多重極展開について考察しようと思う。
▷ [研究部会 OS] 応用カオス(3) [9月3日:15:00-16:20:A](座長:奥富 秀俊(東芝情報システム))
- あるマスター方程式から導出される期待値方程式に対する接触幾何学的記述 / ○後藤 振一郎 (京都大学), 日野 英逸 (統計数理研究所) [概要]
本講演では、離散状態が目標分布であるような系を実現するためのマルコフ連鎖モンテカルロ法の微分幾何学的記述を行う。特に、あるクラスのマスター方程式から期待値が満たす力学系を厳密に求め、その系の非平衡状態を接触幾何学を用いて記述する。その力学系を接触多様体上のベクトル場で記述し、かつ計量を導入し、緩和への収束が指数関数的になることを示す。
- ◎Adaptive Extra Chance Hamiltonian Monte Carlo / ○奥戸 道子 (東京大学), 鈴木 秀幸 (大阪大学) [概要]
Hamiltonian Monte CarloはHamilton系の時間発展をサンプル生成に利用したMCMCであり,Hamilton系の性質を利用して高いサンプリング効率を実現している.本研究では,サンプル生成のダイナミクスを時間発展させる長さを適応的に変化させることで,計算時間を抑えながらサンプル棄却率を下げる手法を提案する.MCMCのサンプリングの正当性を保証したまま,Hamilton系の数値計算の数値誤差を用いてダイナミクスの時間発展の長さを決定する.
- ◎統計量によるPeak-to-Average Power Ratioの上界 / ○津田 宏史 (京都大学 情報学研究科), 梅野 健 (京都大学 情報学研究科) [概要]
Orthogonal Frequency Multiple Access (OFDM)は4G/LTEやWifiなどに用いられているシステムであり、広く使われている無線通信システムである。このOFDMシステムにはPeak-to-Average Power Ratioが大きいという問題がある。一般にPAPRは累積確率分布により測られるため、この曲線の理論値、近似値を求めることは非常に重要な課題である。特に、送信シンボルがある分布から独立に選ばれるような場合に関しては近似曲線が求められている。しかしながら、そうではなく、例えば誤り訂正符号使用時などといった場合は求まってはおらず、複雑な上界が求められているだけである。本研究では、このPAPRの累積確率分布の上界を、送信シンボルの統計量を用いて表す。これは、送信シンボルのセットさえ分かれば、事前にPAPRの曲線の上界を知ることができることを表している。
- 普遍超一般化中心極限定理 / ○梅野 健 (京都大学大学院情報学研究科数理工学専攻) [概要]
中心極限分布をコーシー分布等の分散が存在しない一般のべき則に適応する一般化中心極限定理は良く知られている。
著者等(Shintani-Umeno,2018)は、最近、同一のべき指数を持つ異なるべき則の和が極限で安定分布に収束する超一般化中心極限定理を発見した。この講演では、それを更に異なるべき指数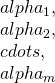 (但し、
(但し、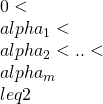 )をもつ一般のべき則(べき指数の種類
)をもつ一般のべき則(べき指数の種類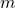 は有限と仮定)した時にも、極限が最小のべき指数
は有限と仮定)した時にも、極限が最小のべき指数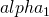 の安定分布
に収束する”普遍超一般化中心極限定理(Universal Super Generalized Central Limit Theorem (USGCLT)”-超一般化中心極限定理 (Super Generalized Central Limit Theorem (SGCLT))を更に普遍化したもの-が成立することを示す。この定理は従って、
べき則をもつデータ(株価の対数収益率データ等)の安定分布に収束すると言うデータ解析によって知られた事実を説明するものとなる。
の安定分布
に収束する”普遍超一般化中心極限定理(Universal Super Generalized Central Limit Theorem (USGCLT)”-超一般化中心極限定理 (Super Generalized Central Limit Theorem (SGCLT))を更に普遍化したもの-が成立することを示す。この定理は従って、
べき則をもつデータ(株価の対数収益率データ等)の安定分布に収束すると言うデータ解析によって知られた事実を説明するものとなる。
▷ [研究部会 OS] 応用可積分系(1) [9月3日:11:00-12:20:E]
- 相似可積分幾何を用いた対数型美的曲線の空間曲線への拡張 / ○梶原 健司 (九州大学マス・フォア・インダストリ研究所), Schief Wolfgang (University of New South Wales) [概要]
美的特性をもつ平面曲線として意匠設計で用いられる対数型美的曲線(LAC)を取り上げ,その空間曲線への一つの一般化を提案する.LACは相似平面幾何の枠組みでは不変パラメータ(角函数)保存可積分変形の定常流,すなわちユークリッド幾何におけるオイラーの弾性曲線の相似幾何類似として特徴付けられ,フェアリング汎函数と呼ばれる汎函数に対する変分原理で定式化することができる.この立場から素直にLACを空間曲線に拡張する.すなわち,相似幾何における空間曲線の不変パラメータ保存可積分変形の定常流として特徴付けられる曲線を考える.曲線の相似捩率はオイラーの弾性曲線と同じ方程式を満たし,(ユークリッド)曲率半径は相似捩率をポテンシャルに持つラメ方程式を満たす.さらに,この曲線に対する変分原理による定式化を与える.
- ◎Fairing of discrete planar curves with integrable discretization of Euler’s elasticae / ○GRAIFF ZURITA SEBASTIAN ELIAS (九州大学大学院数理学府), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
Inspired by the work of Brander et al (2016) on the approximation of planar curves by the elastic curves, we consider its discrete version. Namely, given a general discrete planar curve, we provide an integrable discrete elastic curve which minimizes the 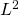 -distance between both curves. Starting with a complete characterization of a generic integrable discrete elastic curve, we construct a curve fitting-like algorithm using seven parameters. The fairing process suffers local minima, which gives rise to numerical instability on some examples. It is shown that the initial guess of the parameters is crucial, and we suggest an algorithm to provide a better guess.
-distance between both curves. Starting with a complete characterization of a generic integrable discrete elastic curve, we construct a curve fitting-like algorithm using seven parameters. The fairing process suffers local minima, which gives rise to numerical instability on some examples. It is shown that the initial guess of the parameters is crucial, and we suggest an algorithm to provide a better guess.
- Lotka-Volterra flow on discrete centroaffine plane curves / ○朴 炯基 (九州大学大学院), 梶原 健司 (九州大学), 松浦 望 (久留米工業大学) [概要]
We formulate basic theoretical frameworks of discrete centroaffine plane curves. Then we consider smooth isoperimetric deformations of discrete centroaffine plane curves, and show that a simple motion is described by the Lotka-Volterra equation. The Miura transformation, between the Lotka-Volterra flow on discrete centroaffine plane curves and the semi-discrete KdV flow on discrete equicentroaffine plane curves, is also constructed.
- Kahan-廣田-木村型離散three wave systemとQRT写像 / ○高江 宥光 (京大数理), 木村 欣司 (サレジオ高専), 中村 佳正 (京大数理) [概要]
非線形光学, プラズマ物理の分野に現れる偏微分方程式として, 三波方程式がある.
三波方程式から空間微分の項を消去すると, three wave systemを得ることができる.
Surisらは, three wave systemに対して, Kahan-廣田-木村離散化法をおこない,
離散three wave systemを導入した. さらに, そのsystemの3つの独立な保存量を得ることに成功している.
しかし, 解についての議論は, 行っていない.
本講演では, ある変数を導入すると, その変数がQRT写像に従うことを示す.
▷ [研究部会 OS] 応用可積分系(2) [9月3日:13:30-14:50:E]
- 戸田格子におけるポアンカレ不変量 / ○佐々 成正 (原子力機構) [概要]
これまで我々は、シンプレクティック数値積分法が相空間の面積和、
すなわちポアンカレ不変量を保つ計算法である事を利用して、PDEに対する運動量保存計算手法について述べてきた。本講演では、戸田格子方程式にこの手法を適用し、ハミルトン格子系に対するポアンカレ不変量
の計算手法を提案する。
- ◎ベルヌイ分布と正規分布を重ね合わせた制約ボルツマンマシンにおける相転移と秩序パラメータ / ○舘崎 優人 (宇都宮大学大学院工学研究科情報システム科学専攻), 上村 佳嗣 (宇都宮大学大学院工学研究科情報システム科学専攻), 小池 正史 (宇都宮大学大学院工学研究科情報システム科学専攻), 矢嶋 徹 (宇都宮大学大学院工学研究科情報システム科学専攻) [概要]
本研究では、制約ボルツマンマシンの相転移点での探索とその付近での振る舞いを、情報統計力学的手法により解析する。幅広いモデルへの応用を視野に入れるため、系を構成するスピンの分布としてベルヌイ分布と正規分布の重ね合わせを行う。秩序パラメータを数値計算し、制約ボルツマンマシンの記憶容量を評価する。
- 正多面体上のハミルトン閉路に対応する離散ソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専), 亀高 惟倫 (阪大名誉教授), 關戸 啓人 (京大) [概要]
プラトンの正多面体の頂点と辺に着目し、ある頂点から一筆書きに全ての頂点を通過して元の頂点に戻る経路である、ハミルトン閉路に着目する。ハミルトン閉路となる辺に重み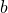 を付け、そうでない辺には別の重み
を付け、そうでない辺には別の重み を付け、離散ラプラシアン行列を導出し、対応する離散ソボレフ不等式の最良定数を求めた。最良定数は、離散ラプラシアン行列の一般化逆行列である、グリーン行列の対角成分の最大値で求めることができる。
を付け、離散ラプラシアン行列を導出し、対応する離散ソボレフ不等式の最良定数を求めた。最良定数は、離散ラプラシアン行列の一般化逆行列である、グリーン行列の対角成分の最大値で求めることができる。
- ◎順序付きハミンググラフにおける量子ウォークについて / ○三木 啓司 (気象大学校), 辻本 諭 (京都大学大学院情報学研究科), Luc Vinet (Université de Montréal) [概要]
代表的なアソシーエションスキームであるハミングスキームの拡張の一つとして順序付きハミングスキームが提案されている.本発表では,順序付きハミングスキームが多変数の直交多項式と自然と結びつくことを示し,スキームから導かれるグラフ上での量子ウォークについて解析を行う.
▷ [研究部会 OS] 応用可積分系(3) [9月3日:15:00-16:20:E]
- Pitman変換による箱玉系の解析 / Croydon David (京都大学大学院情報学研究科), 佐々田 槙子 (東京大学大学院数理科学研究科), 加藤 毅 (京都大学大学院理学研究科), ○辻本 諭 (京都大学大学院情報学研究科) [概要]
高橋・薩摩の箱玉系と確率論におけるPitman変換との関係を明らかにすることで,ランダムな初期値の下での箱玉系について解析を加える.
この中で,両無限の箱玉系への拡張とその連続極限についても議論を加える予定である.
- ◎番号付き・運搬車付き箱玉系のもう1つの一般化 / ○前田 一貴 (関西学院大学理工学部) [概要]
箱玉系の拡張ルールとして,玉に番号をつける拡張,運搬車の容量を制限する拡張があり,その両方の拡張を持つ一般化箱玉系が可解格子模型と深く関係することはよく知られた事実である.本講演では,この両方の拡張を持つ,既知のものとはまた別の一般化を考え,非自励離散KP格子や非自励離散2次元戸田格子との関係を議論する.
- ◎時間2階max方程式の解について / ○山本 惇太郎 (早稲田大学大学院数学応用数理専攻), 高橋 大輔 (早稲田大学大学院数学応用数理専攻) [概要]
離散的計算モデルの1種であるセルオートマトンはmax表現を用いて実数拡張ができ、時間1階の解に関しては過去に研究されている。そこで時間を2階に拡張した場合の解の構造を分析し、その複雑さに応じて分類をした。加えて数値計算により時間発展を解析し、どのようなパターンが現れるか探索した。
- ◎Laurent双直交多項式に付随する可積分系とその正値解について / ○小林 克樹 (京都大学大学院 情報学研究科), 前田 一貴 (関西学院大学 理工学部 数理科学科), 辻本 諭 (京都大学大学院 情報学研究科) [概要]
Laurent双直交多項式に付随する可積分系を導き, その正値な(減算を含まない)時間発展および正値解を与える.
また, この正値解の漸近挙動を解析し, この可積分系がある行列に対する一般化固有値問題計算アルゴリズムになっていることを示す.
さらに, 上記の可積分系の超離散化によってソリトン・セルオートマトン(SCA)を導出し, その解を与える.
このSCAの保存量はYoung図形によって解釈でき, 各行の大きさがソリトンの振幅に対応することを見る.
▷ [研究部会 OS] 応用可積分系(4) [9月3日:16:30-17:50:E]
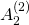 型クラスター代数の生成元について / ○野邊 厚 (千葉大学教育学部) [概要]
型クラスター代数の生成元について / ○野邊 厚 (千葉大学教育学部) [概要]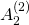 型クラスター代数のミューテーションは保存量をもつ2次元離散可積分系と見なすことができる。離散可積分系の初期値問題を解くことにより、クラスター代数の生成元を具体的に構成する。
型クラスター代数のミューテーションは保存量をもつ2次元離散可積分系と見なすことができる。離散可積分系の初期値問題を解くことにより、クラスター代数の生成元を具体的に構成する。
- ◎要素指定逆固有値問題に関する一意解のII型離散ハングリー系を利用した解法 / ○上田 純也 (同志社大学大学院理工学研究科), 近藤 弘一 (同志社大学大学院理工学研究科) [概要]
要素指定を伴う下ヘッセンベルグ型帯行列に関する逆固有値問題を考える.
一意な行列が存在し,かつ有限ステップのアルゴリズムが構成可能なことを示す.
これをII型の離散ハングリー戸田方程式の一般解を利用して示す.
▷ [研究部会 OS] 折紙工学(1) [9月3日:09:30-10:50:D]
- 超長部材の圧潰特性に関する一考察 / ○陳 暁詩, 楊 陽, 趙 希祿, 萩原 一郎 [概要]
自動車のエネルギー吸収材の700mmに対し、土木建築で使用されるエネルギー吸収材は3000mm程度と長い。
いずれも中空断面材が使用されるが、折れ曲がりやすい。
自動車のエネルギー吸収材ではビードを利用したが、土木建築用ではこの手法の踏襲は不可である。捩って得られる折紙構造で対応することを提案する。
- 等面四面体の source unfolding / ○山岸 義和 (龍谷大学), 西崎 惇也 (龍谷大学), 佐治 拓道 (龍谷大学) [概要]
凸多面体上で、一点 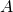 からの測地的距離による cut locus を考えると、source unfolding と呼ばれる展開図が得られる。
等面四面体の source unfolding は、平面のタイル張り(ボロノイ分割)を与える。等面四面体で、source unfolding が六角形とならないような基準点
からの測地的距離による cut locus を考えると、source unfolding と呼ばれる展開図が得られる。
等面四面体の source unfolding は、平面のタイル張り(ボロノイ分割)を与える。等面四面体で、source unfolding が六角形とならないような基準点 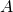 の集合(分岐点集合)は、面の垂心を端点とする二次曲線および線分の和集合となる。
の集合(分岐点集合)は、面の垂心を端点とする二次曲線および線分の和集合となる。
- ◎展開立方体折紙による宇宙構造システム構築のための構造座屈の調査 / ○有田 祥子 (静岡大学), 宮崎 康行 (日本大学), 福田 一樹 (静岡大学), 山極 芳樹 (静岡大学) [概要]
新たな展開宇宙構造技術の確立に向け,本研究では円筒ねじり折りの一種である展開立方体折紙構造を利用した構造システムを提案した.軽量・省スペースでありながら,立方体各面に膜面デバイスを配置できる,モジュールの連結により大型構造の構築が可能となるなど,宇宙利用に向けて有用な構造システムである.本発表では展開中に大変形する部材の座屈メカニズムを解析によって示した結果を発表する.
- 折紙ロボットで折るための展開図 / ○ルイス ディアゴ (明治大学), 楊 陽 (明治大学), ジュリアン アンドレス ロメロ (AZAPA), 萩原 一郎 (明治大学) [概要]
これまでの折紙設計ソフトは、人間が折ることを前提に作られるものであるが、人間より器用さで劣る折紙ロボットで折るための折紙用2次元展開図について議論する。
そのための一つのキーワードは木構造であるが、必ずしも木構造は必要条件ではないことから真の必要条件を探る。
▷ [研究部会 OS] 折紙工学(2) [9月3日:11:00-12:20:D]
- 果物の入った箱入りアッセンブリトラスコアの輸送に関する一考察 / ○阿部 綾 (明治大学), 寺田 耕輔 (奈良高専), 萩原 一郎 (明治大学) [概要]
今後、需要が見込まれる輸送形態として、イチゴのような高級志向の農産品の航空輸送やドローンによる配達といったものがある。そこで新しい梱包材として、再利用可能なことや緩衝材としての機能も兼ねることからATCPを用いることにメリットが大きいと考えられる。従来の梱包材と比してATCPの梱包材としての優位な機能について解析を行い、実用化について検討する。
- 編み紙の数理 ∼材料の伸びを考慮した曲面設計最適化∼ / ○堀川 由人 (大阪大学工学研究科), 垂水 竜一 (大阪大学基礎工学研究科) [概要]
紙などの薄い材料から曲面形状を構成する際には, 曲面を曲面片に分割して, それぞれの曲面片を切り出す必要がある. 先行研究では曲面片を可展面に近似する手法に限られていたが, 本研究では紙の弾性特性を活かした最適化手法を提案する.
- ねじり折り平坦可折定理の証明の完成 / ○川崎 英文 (九州大学) [概要]
ねじり折りが平坦可折であるための必要十分条件は,周囲の帯で定義されるホールが空にならないことである(ねじり折り平坦可折定理).これまでは,一定の仮定の下で定理の証明を与えたが,本講演ではそれらの仮定を外し証明を完成させる.証明で用いる数学は,凸解析のHellyの定理とGaleの二者択一の定理,Brouwerの不動点定理と同値なKKM定理である.
- 6次元のかたち巡り / ○宮崎 興二 (京都大学名誉教授) [概要]
正八面体群あるいは正二○面体群の対称性を持って広がる6本の直線を、6次元空間の直交座標軸の3次元空間への直投影と考え、その座標軸に基づいて、さまざまな6次元多胞体を作図し折紙模型を作る。最終目的はかたちで見る6次元空間の重大性の指摘にある。
▷ [研究部会 OS] 科学技術計算と数値解析(1) [9月5日:09:30-10:50:D]
- ◎反応拡散方程式に対する修正Strang splitting解法について / ○中野 航輔 (名古屋大学), 宮武 勇登 (大阪大学), 剱持 智哉 (名古屋大学), 曽我部 知広 (名古屋大学), 張 紹良 (名古屋大学) [概要]
本講演では,反応拡散方程式の時間変数の離散化について考える.
Strang splitting解法は多くの場合2次精度が期待される離散化手法だが,
反応拡散方程式に対しては,境界条件によっては精度の劣化がみられる.
そこで本講演では,精度の劣化の改善を目的とした修正Strang splitting法を提案し,
数値実験を通して精度の改善が得られたことを報告する.
- ◎滑らかな領域上のRobin境界条件を持つPoisson方程式に対するNitsche法 / ○千葉 悠喜 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
滑らかな領域上の問題を数値計算で近似解を計算する場合,有限要素法では領域を多角形などで近似して計算を行っている.
このとき,近似の仕方によっては元の問題と異なる問題の近似解を求めてしまうことがある.
特に,境界条件に微分が含まれる問題では,より一層の注意が必要である.
標準的な有限要素法では,様々な境界条件の下の誤差について解析されている一方,Nitsche法などではそのような解析が行われていない.
本研究は,滑らかな領域上のRobin境界条件を持つPoisson方程式に対し,Nitsche法の適用とその解析を行う.
- ◎離散化誤差を考慮した常微分方程式の初期値推定について / ○松田 孟留 (東京大学), 宮武 勇登 (大阪大学) [概要]
常微分方程式で記述される現象において、観測データをもとに初期値を推定するのは基本的な問題である。この問題に対して、ルンゲクッタ法などで得られる数値解を観測データに当てはめる方法が考えられるが、数値解に含まれる離散化誤差が推定精度に与える影響は明らかでない。たとえば、高次元の常微分方程式においては計算量の観点から時間刻みを十分小さくとれないため、離散化誤差を無視できないと考えられる。そこで本研究では、数値解法の性質(次数、保存性など)と初期値推定量の統計的性質(一致性、有効性など)の関係について考察する。
- 微分代数方程式に対する離散勾配法の構築 / ○佐藤 峻 (東京大学) [概要]
微分代数方程式 (DAE) は常微分方程式 (ODE) の一般化であり,各種の現象のモデリングにおいて自然に現れる.拘束条件付き機械系はその好例であり,力学的エネルギー保存則が成立するため,この性質を受け継いだ数値解法が構築・利用されている.この研究は,ODEにおける保存的数値解法に関する豊富な研究の観点からも自然なものであるが,DAEにおける研究は未だ黎明期にあり各論に止まっている.本研究では,ある種の仮定の下で,拘束条件と保存則を同時に保つ離散勾配法を統一的に構築できることを示す.
▷ [研究部会 OS] 科学技術計算と数値解析(2) [9月5日:11:00-12:20:D]
- ◎非双曲型平衡点を持つ力学系におけるLyapunov関数の精度保証による構成について / ○寺坂 元 (電気通信大学 情報・ネットワーク工学専攻), 中村 正男 (電気通信大学 情報・ネットワーク工学専攻), 新田 光輝 (電気通信大学 情報・ネットワーク工学専攻), 山本 野人 (電気通信大学 情報理工学研究科) [概要]
連続力学系の双曲型平衡点の近傍では二次形式によるLyapunov関数が構成可能であり、精度保証に依る構成法もいくつか知られている。これに対し、非双曲型平衡点の近傍では、二次形式のLyapunov関数は原理的に構成することができない。本講演では、 非双曲な平衡点に持つ力学系を扱う。常微分方程式右辺のTaylor展開を考え、そこから高次項を切り捨てた系を構成する。この系のLyapunov関数を構成し、これが元の力学系でもLyapunov関数となっているかを精度保証で検証する。
- ◎精度保証付き数値計算による高次元力学系の安定・不安定多様体の捕捉について / ○新田 光輝 (電気通信大学), 山本 野人 (電気通信大学) [概要]
本講演では、高次元力学系の安定多様体・不安定多様体の捕捉を行う精度保証法を考案する。これは、Brouwerの一致点理に基づき、写像度の精度保証を利用した新しい方法である。また、本手法を実際に適用した例についても紹介する。
- ◎高次元半線形熱方程式の球対称問題に対する有限要素法の誤差解析 / ○中西 徹 (東京大学大学院数理科学研究科), 齊藤 宣一 (東京大学大学院数理科学研究科) [概要]
高次元半線形熱方程式の球対称解を計算するために対称有限要素近似および非対称有限要素近似を考え、その重み付き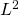 ノルムと
ノルムと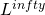 ノルムでの誤差解析の結果を報告する。
ノルムでの誤差解析の結果を報告する。
- 数値積分を用いるLagrange-Galerkinスキームの収束性 / ○内海 晋弥 (早稲田大学), 田端 正久 (九州大学(名誉教授)) [概要]
Navier-Stokes問題のための数値積分を用いるLagrange-Galerkinスキームを考える.これまでにこのスキームの収束性は示されていなかった.本報告では,時間刻みが十分小さい条件の下で収束性を示す.
▷ [研究部会 OS] 科学技術計算と数値解析(3) [9月5日:13:30-14:50:D]
- 代用電荷法による複素平面から3次元曲面への写像 / ○岡野 大 (愛媛大学) [概要]
複素平面中の領域から3次元曲面への写像を境界同士の対応関係 を境界条件とする調和関数によって行うことができる。
近似調和関数の計算に代用電荷法を用いる方法とその応用について説明する。
- ◎代用電荷法におけるFekete点の近似 / ○平野 広明 (東京大学), 田中 健一郎 (東京大学) [概要]
偏微分方程式の数値解法の一つ,代用電荷法(基本解近似解法)における拘束点配置問題を取り扱う.拘束点の配置としてFekete点を用いると高精度な結果が得られることが知られているが,その簡単な求め方は知られていない.本研究では,Fekete点を与える最適化問題を凸最適化問題に近似し,近似的にFekete点を求める手法を構成する.そして,数値的に求めた近似Fekete点を拘束点に用いた数値実験結果を示す.
- 再生核ヒルベルト空間における関数近似のための標本点生成法について / ○田中 健一郎 (東京大学) [概要]
正定値核によるデータや関数値の補間は,様々な分野で基礎的な手法として用いられている.正定値核には再生核ヒルベルト空間(RKHS)が対応することが知られており,この空間において,補間の近似精度を数学的に評価することができる.そして,このような数学的評価に基づくと,補間に用いる標本点を,近似精度が向上するように生成することができる.この標本点生成については,先行研究では貪欲法が考案され使用されていることが多い.一方,本研究では,近似や緩和を用いて,標本点を求める問題を凸最適化問題に帰着し,それを解くことで全体的なバランスの良い標本点を生成する方法を提案する.
- 連分数を用いた数値解析接続とFourier変換への応用 / ○緒方 秀教 (電気通信大学大学院情報理工学研究科情報・ネットワーク工学専攻) [概要]
本講演では、冪級数で与えられた解析関数を連分数展開により解析接続する方法を提案し、理論・実験両面からその性能を検証する。また、この数値解析接続と佐藤超函数論を用いてFourier変換を数値計算する方法についても触れる。
▷ [研究部会 OS] 科学技術計算と数値解析(4)(〜16:40) [9月5日:15:00-16:20:D]
- 微圧縮超弾性体の大変形問題に対する近傍問題の構成 / ○山田 貴博 (横浜国立大学) [概要]
筆者等はRoy等が提案する近傍問題法(Method of Nearby Problems)を固体の非線形問題に適用した数値解の検証手法を開発してきた.本研究ではこの手法をゴム材料に対応する微圧縮超弾性体の大変形問題に適用する.特に微圧縮体の近傍解を構成する際には,体積変形に対する制約条件を考慮しなければならないことを数値計算結果により示す.
- ◎オフセット角度を用いた断層画像再構成における厳密解の構成法 / ○神田 直大 (芝浦工大/理化学研究所), 高梨 宇宙 (理化学研究所) [概要]
CT-scanをはじめとする断層画像技術の根幹の一つをなすのがラドン変換である。実際の測定は離散化されており、画像を得る操作は離散化したラドン逆変換の作用により実現する。この逆変換による再構成像は一般に一意に決定されないことが経験的に知られている。この為、画像再構成は逐次代入計算に基づき実行され、計算コストを増大させる一因となっている。我々は、データサンプリング方法を改良することにより、厳密な逆変換を得る一つの方法を提案する。
- ◎抵抗率測定に使用される四探針法の数理モデルの解析:有限要素解のHypercircle法による誤差評価 / ○中野 泰河 (新潟大学大学院 自然科学研究科 数理物質科学専攻 数理科学コース), 劉 雪峰 (新潟大学大学院 自然科学研究科) [概要]
四探針法は半導体材料の抵抗率を測定するために使用される方法である。
本研究では探針と材料の接触条件に関して幾つかの物理的な仮定に応じて、微分方程式の境界値問題による数学的モデルを提案した。
さらに、各数学的モデルに応じて、Hypercircle法による有限要素解の誤差評価を行った。
- ◎抗原・抗体の体内動態の定量的解析に向けたモデルパラメータの 多様性に対する考察 / ○小松 瑞果 (神戸大学大学院システム情報学研究科), 谷口 隆晴 (神戸大学大学院システム情報学研究科/JST さきがけ) [概要]
講演者らは,これまでの研究の中で,抗原・抗体の体内動態を定量的に解析するための数理モデルを構築してきた.一般に,このようなモデルでは,パラメータの数に対してデータが十分でないことが多く,パラメータ推定の結果が一意に定まらない.本講演では,そのようにして得られた,様々なパラメータの値についての考察を行う.
- ◎アンケートデータを用いた交流ネットワーク推定手法 / ○佐藤 智久 (神戸大学), 谷口 隆晴 (神戸大学), 増本 康平 (神戸大学), 近藤 徳彦 (神戸大学), 岡田 修一 (神戸大学) [概要]
近年,様々なデータが取得できるようになってきたことを背景に,人々の
交流の様子をネットワークで表現し,そのつながりを解析することが重要
となってきている.このようなネットワークの構造を決定するためには,
詳細なデータの取得が必要であるが,これには,大きな経済的,人的コス
トが生じる.本研究では,より取得が簡単な,アンケートデータを用いて
交流の様子を推定する手法について述べる.
▷ [研究部会 OS] 機械学習 [9月3日:09:30-10:50:E]
- カーネルリッジ回帰による物質・材料研究 / ○田村 亮 (物質・材料研究機構/東京大学) [概要]
現在,物質・材料科学分野ではデータ駆動型研究が注目されている.本講演では,機械学習手法の一つであるカーネルリッジ回帰を利用した物質・材料研究として,第一原理計算を入力とした機械学習力場構築及び,ニオイセンサーのシグナル解析を紹介する.
- 時空間データ解析のための自己回帰テンソル分解 / ○竹内 孝 (NTT) [概要]
時空間データ解析では,いつ・どこでデータが観測されたかという情報を用いて,データの未観測場所での過去観測値の補完や将来の観測値の予測などが行われている.テンソル分解法は,複数種類の観測データが扱え,欠損データが存在していても解析が可能であり,効率的なアルゴリズムが存在するなどの利点があるため,時空間データの解析で多く利用されている.しかし,現在までデータ未観測場所の将来観測値の予測問題のためのテンソル分解の手法は提案されていない.本研究では,上記問題に取り組むために,空間情報を用いた自己回帰正則化を定式化し,さらにテンソル分解の正則化として利用する自己回帰テンソルの提案をおこなう.実世界で観測されたタクシー降車データおよびバイクシェアリングデータを用いた実験により,提案手法の優位性を定量的・定性的に示す.
- ◎Selective Inferenceに基づく変化点検出とその応用 / ○梅津 佑太 (名古屋工業大学), 竹内 一郎 (名古屋工業大学/理化学研究所/物質・材料研究機構) [概要]
多次元系列から共通の変化点を検出する場合, 1次元系列に統合された系列をスコアと考え, そのスコアを最大化する点として変化点を探索することが多い. ところで, 検出した統計的有意性を評価する場合,スコアの最大値の分布を導出する必要があるが, たとえ漸近的であっても, その導出は困難となる. 本研究では, 変化点検出が探索と推論の2段階で解析されるものと捉え, 近年提案されたselective inferenceの枠組みで, 妥当な検定問題を定式化する.
- ◎関数推定の理論に基づく深層学習の原理解析 / ○今泉 允聡 (統計数理研究所) [概要]
本研究は、深層学習が高精度を発揮する原理の解析を行う。深層学習はデータ分析で高い精度を発揮することから、社会の各領域において実用が進んでいる。しかし、なぜ他手法より高い精度を達成できるのか、その原理の大部分はまだ明らかになっていない。本研究は、データから未知関数を推定する統計理論を用い、他手法の多くが最適精度を達成できないある状況下で、深層学習が理論上の最適精度を達成することを証明し、その優位性を明らかにした。
▷ [研究部会 OS] 行列・固有値問題の解法とその応用(1) [9月4日:09:00-10:20:D](座長:相島 健助(法政大学))
- 複素モーメント型教師あり次元削減法 / ○今倉 暁 (筑波大学), 松田 萌望 (筑波大学), 叶 秀彩 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
本講演では,高次元特徴量を持つデータのクラスタリングやクラシフィケーショ ン手法として,行列のトレースの最大化・最小化に基づく次元削減法のアイディ アを基盤とした新しい複素モーメント型の教師あり次元削減法を提案する.提案法は,分類性能の改善を目的とし,行列のトレースと二乗誤差を組み合わせ た新しい目的関数を導入し,複数固有ベクトルを含む複素モーメント型部分空間 上の最小化問題として定式化される.
- ◎相互作用型の残差スムージングによる積型BiCG法の収束性改善 / ○相原 研輔 (東京都市大学) [概要]
最近,反復法の残差ノルムの収束振る舞いを改善するスムージングについて,新しい計算スキームが提案された.これは,行列ベクトル積から発生する丸め誤差の蓄積を抑えるように,スムージング前後の反復列を相互作用させるものであり,CGS法の収束性を大幅に改善できることが示されている.本発表では,同様の手法をBiCGSTAB法など他の積型解法に適用した新しいアルゴリズムを提案する.数値実験により提案した方法の有効性を示す.
- Block BiCGSTAB法の近似解高精度化と数値的安定化 / ○多田野 寛人 (筑波大学), 倉本 亮世 (筑波大学) [概要]
Block BiCGSTAB法は複数本の右辺ベクトルをもつ連立一次方程式の数値解法の一つであり,反復回数,計算時間の観点で効率的な解法である.
しかしながら,右辺ベクトル数が多い場合は,残差の偽収束による近似解精度低下,及び数値的不安定性の増大により残差が収束しないことがある.
本講演では,同法の残差の偽収束を抑える漸化式の構築方法,及びその数値的安定性向上法について述べる.
- 一般化非定値固有値問題へのシルベスター慣性則 / ○中務 佑治 (国立情報学研究所), Noferini Vanni (University of Essex) [概要]
シルベスターの慣性則は通常対称固有値問題に対して定義され,合同変換が(正,負,0)固有値の数を保つことである.実数区間内の固有値数を計算する等に応用できる.一般化固有値問題に対しても,一つの行列が正定値であれば同じ結果が適用できる.本研究では正定値でない一般化固有値問題に対しても近い結果が成り立つことを示す.具体的には,合同変換は(正,負,0)の固有値数を保存しないが,これらが変化する度合いには非自明な上限下限が存在することを示す.
▷ [研究部会 OS] 行列・固有値問題の解法とその応用(2)(〜12:10) [9月4日:10:30-11:50:D](座長:中務 佑治(国立情報学研究所))
- ◎非線形固有値問題に対するblock Arnoldi法 / ○長坂 英明 (慶應義塾大学理工学研究科基礎理工学専攻), 野寺 隆 (慶應義塾大学理工学部数理科学科) [概要]
本発表は非線形固有値問題の近似解法について考える,このような問題は,流体力学などで登場し,通常,この近似解法として反復法であるArnoldi法を発展させた無限Arnoldi法が用いられることが多い.その理由は解法の安定性が比較的高いことである.本発表では,このような問題に対して,block無限Arnoldi法と非対称無限Lanczos法を提案する.具体的な問題の数値実験を通して従来手法と比較検討し,提案手法の有効性を示す.
- 少数のレゾルベントの線形結合の多項式をフィルタとして用いた一般固有値問題の解法 / ○村上 弘 (首都大学東京) [概要]
フィルタを用いて対称定値一般固有値問題の固有対で固有値が指定区間にあるものを解く.
フィルタには少数のレゾルベントの線形結合の多項式をうまく調整して用いる.
多項式にはチェビシェフ多項式を用いてフィルタの設計と構成を簡易なものにする.
レゾルベントの作用を与える連立1次方程式を解くのに直接法を用いる場合には,
演算量の大部分を行列分解が占めるので,用いるレゾルベントの数が少ないと演算量の面からは有利になる.
- 対称固有値問題を解く反復射影法に対して収束を保証するリスタートについて / ○相島 健助 (法政大学) [概要]
一般的に,大規模対称固有値問題の数値解法には射影法が用いられる.射影のための低次元部分空間の生成においては,反復的に部分空間を更新して目的の固有空間を特定するのが標準的な手法になる.本発表では,リスタートを導入した反復射影法に対する収束性について議論する.特に,線形方程式の近似解により部分空間を生成する反復射影法に焦点を当て,リスタートに調和Ritzベクトルを用いる場合の収束を理論保証する定理を与える.
- ◎実対称疎行列に対する効率的三重対角化アルゴリズム / ○廣田 悠輔 (東京電機大学) [概要]
実対称疎行列の固有値および対応する固有ベクトル(固有対)を求めるにはLanczos法などの反復アルゴリズムを用いるのが普通である.しかしながら,このような反復アルゴリズムは非常に多数の固有対を求めるのには適していない.本研究では,Bischofらによる帯行列reductionアルゴリズム(2000)に変更を加えることで,ある種の疎構造をもつ疎行列に対して効率的な三重対角化が可能であることを示す.また,一般の実対称疎行列に対する効率的な三重対角化に向けた展望について述べる.
- 荻田・相島の固有ベクトル反復改良法における重複固有値の扱いについて / 白間 久瑠美 (電気通信大学), 工藤 周平 (電気通信大学), ○山本 有作 (電気通信大学) [概要]
荻田・相島により最近提案された実対称行列の固有ベクトル反復改良法は、近似固有値・固有ベクトルの精度を向上させるための効率的な手法である。同手法のうち、単純固有値に対するアルゴリズムは導出が明快であるが、重複固有値に対するアルゴリズムは、直感的な理解が困難である。本発表では、重複固有値に対する同手法のアルゴリズムを、より理解しやすい形で導出することを試みる。
▷ [研究部会 OS] 計算の品質(1)(14:10〜) [9月3日:14:10-14:50:D](座長:山中 脩也(明星大学))
- ◎高精度行列‐行列積のためのBatched BLASおよび疎行列演算を用いた実装方式のGPU環境での性能評価 / ○石黒 史也 (名古屋大学大学院 情報学研究科), 片桐 孝洋 (名古屋大学 情報基盤センター), 大島 聡史 (九州大学 情報基盤研究開発センター), 永井 亨 (名古屋大学 情報基盤センター), 荻野 正雄 (名古屋大学 情報基盤センター) [概要]
本発表では,倍精度演算による精度を保証する高精度行列-行列積に,複数のBLAS演算をまとめて実行することで演算効率を向上させる,Batched BLASを適用した実装方式を提案する.また,演算途中で密行列から疎行列になる特性を利用した「疎行列-密行列」実装方式の性能評価を行う.東京大学に設置されたReedbush-H システムのGPU環境を利用し,以上の2実装の性能評価を行う.
- 分散並列計算環境における疑似多倍長精度演算を用いた行列・ベクトル積の実装と評価 / ○小林 亮太 (芝浦工業大学), 尾崎 克久 (芝浦工業大学) [概要]
本研究では疑似多倍長演算を用いて, 分散並列計算環境における行列・ベクトル積を高精度で計算するルーチンの提案を目的とする. 提案に際してベクトルの総和や内積計算を任意の順序で行っても誤差評価が可能な高精度計算アルゴリズムの提案も併せて行う. なお性能調査は, PBLASの計算ルーチンPDGEMVを比較対象として, 理研の京や名古屋大学のFX100を用いて行う.
▷ [研究部会 OS] 計算の品質(2) [9月3日:15:00-16:20:D](座長:渡部 善隆(九州大学))
- 厳密な固有値・特異値がわかる行列の生成法 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
本発表では,厳密な固有値が事前にわかるテスト行列の生成法について述べる.昨年度の日本応用数理学会年会ではジョルダン標準形をもとに,上2重対角行列とアダマール行列を用いてテスト行列を生成する手法について発表した.今回は,アダマール行列以外の行列を用いてもテスト行列を生成できる一般化された手法を紹介し,具体的な行列の生成法を紹介する.
- 一般化エルミート固有値問題の周回積分型精度保証付き部分固有値計算 / 今倉 暁 (筑波大学システム情報系), 保國 惠一 (筑波大学システム情報系), ○高安 亮紀 (筑波大学システム情報系) [概要]
本講演では、一般化エルミート固有値問題に対して、その部分固有値を精度保証付き数値計算する方法について紹介する。本手法の特徴はblock Hankel型のSakurai-Sugiura(SS)法を利用することである。SS法によって固有値問題は行列サイズが縮小されたあるHankel行列の一般化固有値問題となり、これを精度保証付き数値計算によって解くことで所望の部分固有値を精度保証付き数値計算できる。
- ◎LU分解を用いたCholeskyQRアルゴリズムの誤差解析 / ○寺尾 剛史 (芝浦工業大学), 尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
我々は、列フルランク行列に対するQR分解のアルゴリズムとその誤差解析について発表する。
近年、高速な手法としてCholeskyQRアルゴリズムを用いた手法が注目されている。
しかし、このアルゴリズムは比較的に小さい条件数で破綻することが知られている。
そこで、LU分解を用いた手法があり、これは悪条件な問題に対して計算を行うことができる。
本発表では、LU分解を用いたCholeskyQRアルゴリズムの丸め誤差解析と数値実験の結果を紹介する。
- 行列積に関する計算順序の特定法とその応用 / ○坂本 篤志 (芝浦工業大学大学院), 尾崎 克久 (芝浦工業大学) [概要]
本発表では,行列積に対する数値計算を扱う.
計算結果は,演算の順序に依存するため,
計算機環境や使用するライブラリが異なれば,
同じ入力に対しても異なる計算結果を得ることがある.
そのため, ある問題を解く際に計算方法が分からない場合は
任意の計算順序に対応する最も悪い誤差評価を使用する必要がある.
そこで, 計算方法が分からない問題に対して例題を与え,
演算結果から順序を特定する方法を幾つか紹介する.
また, それらの方法によって推測できた計算方法を元にした
異なる計算機環境にて再現性ある結果を得る応用例も紹介する.
▷ [研究部会 OS] 計算の品質(3) [9月3日:16:30-17:10:D](座長:田中 一成(早稲田大学))
- 2階楕円型作用素に対する逆作用素ノルム評価の改良 / ○渡部 善隆 (九州大学), 木下 武彦, 中尾 充宏 (早稲田大学) [概要]
2階線形楕円型作用素に対する可逆性の検証と逆作用素ノルムの上界の厳密な評価は,無限次元Newton法に基づく非線形問題の解に対する計算機援用証明において本質的な役割を果たします.本講演ではLaplacianのL2ノルムの上界を与えるための可逆性条件とノルム評価を援用することにより,既存の手法の改良が可能であることを具体的な検証例を用いて示します.
- 微分方程式の爆発解の精度保証付き数値計算:ケーススタディ — 指数関数非線型項を持つ場合 / ○松江 要 (九州大学マス・フォア・インダストリ研究所 / 九州大学カーボンニュートラル・エネルギー国際研究所), 高安 亮紀 (筑波大学システム情報系) [概要]
本講演では指数関数非線型項を持つ微分方程式の爆発解を扱います。
ごく近年、多項式が無限遠方にて支配的となるベクトル場に対して, 爆発解の精度保証付き数値計算や力学系的解釈の理論構築を行ってきました。
そこではベクトル場の漸近的な意味での擬斉次性や時間スケール特異点解消を使って爆発解を幾何学的に解釈し、リャプノフ追跡と呼ぶ精度保証計算のテクニックを用いて爆発時刻の陽な評価を可能としています。
指数関数非線型項を伴う系はこの枠から外れますが、従来のアイデアを素直にアレンジすることで従来の議論をそのまま適用し、爆発解の考察を数学的・数値的に行うことが可能となると期待され、爆発解の特徴付けを可能とする系のクラスを広げる起爆剤となり得ます。
- フーリエ係数の時間発展方程式に対する解の精度保証付き数値計算 / ○高安 亮紀 (筑波大学システム情報系) [概要]
周期境界条件を課した偏微分方程式の初期値境界値問題をスペクトル法で数値計算する際、未知関数のフーリエ級数の各係数に関する時間発展方程式の解を数値計算する。この問題に対して解の精度保証付き数値計算を実行するには、点列空間上に定義された可算無限個の常微分方程式系の初期値問題を厳密に解く必要がある。本講演では、この常微分方程式系に対する解の精度保証付き数値計算法を紹介する。
- 3次元領域におけるNavier-Stokes方程式の定常解の検証 / ○劉 雪峰 (新潟大学), 中尾 充宏 (早稲田大学), 大石 進一 (早稲田大学) [概要]
3次元領域におけるNavier-Stokes方程式の定常解について、計算機での精度保証付き数値計算を用いる解の検証アルゴリズムを提案する。提案方法はこれまでに非線形偏微分方程式の解を検証するために開発された方法(Newton-Kantorovichの定理が中心である)をベースにして、Navier-Stokes方程式の有限要素解の事前誤差評価と微分作用素の固有値評価に関する新しい結果を応用することで、3次元領域におけるNavier-Stokes方程式の定常解の検証が可能となる。
▷ [研究部会 OS] 産業における応用数理 [9月5日:13:30-14:50:B]
- 半導体の抵抗率測定法の開発に現れるいつくかの応用数学の問題 / ○劉 雪峰 (新潟大学大学院自然科学研究科) [概要]
発表者は半導体の抵抗率測定機を開発している会社との共同研究を行っている。この研究では、抵抗率測定に使用される4探針法の数学モデルを検討する。実際の問題を解くためには、幾つかの新しい数学の問題が現れ、様々な数学の理論と計算手法が不可欠であることが分かっている。例えば、ディラックのデルタ関数に関する有限要素法の計算手法と誤差評価が要求される。本発表では、この研究でチャンレンジしている数学の問題を紹介し、考察を行う。
- 半導体製造プロセスにおける悪条件線形方程式の解法 / ○木村 泰己 (東芝メモリ株式会社), 松縄 哲明 (東芝メモリ株式会社), 三本木 省次 (東芝メモリ株式会社) [概要]
半導体製造において、微細な回路パターンを転写するリソグラフィー工程を精度良くシミュレーションする必要がある。
このシミュレーションのモデルは線形方程式に定式化出来る。しかしながら計測データに制約がある為、線形方程式は悪条件となる。
従って、いかに悪条件線形方程式を解くかが課題となっている。
本発表では、行列の前処理と特異値分解による打ち切り最小二乗解が良い結果を示した事、また特異値分解の高速化にはRSDVが有効であった事を報告する。
- 名古屋大学情報基盤センターにおけるスーパーコンピュータ民間利用制度の展開と課題 / ○片桐 孝洋 (名古屋大学情報基盤センター), 田島 嘉則 (名古屋大学情報連携統括本部), 毛利 晃大 (名古屋大学情報連携統括本部), 山田 一成 (名古屋大学情報連携統括本部), 高橋 一郎 (名古屋大学情報連携統括本部), 荻野 正雄 (名古屋大学情報基盤センター), 永井 亨 (名古屋大学情報基盤センター), 服部 昌祐 (名古屋大学情報連携統括本部) [概要]
本発表では、名古屋大学情報基盤センターにおけるスーパーコンピュータ民間利用制度の概要と、平成30年度までの同制度によるスーパーコンピュータ利用の状況について説明するとともに、今後の展開予定と課題について示す。
- ものづくり研究会 活動紹介 / 高田 章 (旭硝子株式会社), 櫻井 鉄也 (筑波大学), ○井手 貴範 (アイシン・エィ・ダブリュ株式会社) [概要]
ものづくり企業に役立応用数理手法の研究会は2014年8月に発足し4期目を迎えました. 本研究会には日本を代表するものづくり企業約20社が参加をしています. 活動の中核は隔月開催される技術セミナーでは,シミュレーション技術,データサイエンスの先端研究, 数理科学分野の若手研究者による成果の講演です.異分野の企業間における交流も活発に行い見学会も実施しています.本公演ではこれまでの活動と将来の展望について紹介をします.
▷ [研究部会 OS] 数理医学(1) [9月5日:09:30-10:50:B]
- ◎血管新生における血管内皮細胞の基本動態に関する数理モデル / ○林 達也 (東京大学大学院数理科学研究科), 由良 文孝 (はこだて未来大学), 間田 潤 (日本大学生産工), 時弘 哲治 (東京大学大学院数理科学研究科), 礪波 一夫 (東京大学大学院医学系研究科), 栗原 裕基 (東京大学大学院医学系研究科) [概要]
血管新生では,一つ一つの血管内皮細胞が複雑な運動を行いながら血管形態を作る.最近の実験から,血管内皮細胞の基本的な運動として,回転運動と直線運動が示唆されている.本発表では,血管内皮細胞の回転運動と直線運動を取り入れた数理モデルを紹介し,数値シミュレーション結果と実験結果の比較検討を行う.
- ◎NF-κB非古典的経路における振動現象の数理的解析 / ○畑中 尚也 (大阪大学基礎工学研究科 システム創成専攻 数理科学領域), 井上 純一郎 (東京大学医科学研究所 癌細胞増殖部門 分子発癌分野), 鈴木 貴 (大阪大学数理・データ科学教育研究センター) [概要]
NF-κBは数百もの生体機能を制御するタンパク質であり,刺激の種類によって古典的経路,非古典的経路という異なる活性化機構を持つ.NF-κBが正常に機能するためには,適切な周期で細胞質-核間を行き来することが必要である.しかし,非古典的経路ではすべての細胞で同一の挙動が得られる訳ではない.我々は,何故細胞ごとに挙動が異なるのかを解明するために数理モデルを構築し解析した.本講演ではNF-κB非古典的経路の振動現象を制御する上で重要なパラメータに関して数理的観点から報告する.
- [特別講演:40分] 数理解析を用いた中心体複製の開始制御機構の解明 / ○中村 貴紀 (東京大学 医科学研究所 分子シグナル制御分野), 西住 紀子 (東京大学 医科学研究所 分子シグナル制御分野), 中澤 嵩 (大阪大学 数理・データ科学教育研究センター), 森 竜樹 (大阪大学 基礎工学研究科), 鈴木 貴 (大阪大学 数理・データ科学教育研究センター), 武川 睦寛 (東京大学 医科学研究所 分子シグナル制御分野) [概要]
細胞内の中心体は、染色体の均等分配を担うことで次世代の娘細胞に正確な遺伝情報を受け継ぐ。中心体数の異常は染色体の不均等分配を誘発して癌の悪性化を招くだけでなく、小頭症や精子形成不全の要因ともなる。このため正常細胞では中心体複製が厳密に制御され中心体数が保持されるが、その分子機構は不明であった。今回我々は数理解析を利用して中心体複製に先行して起こる中心体複製鍵分子の中心体移行機構を解明したので報告する。
▷ [研究部会 OS] 数理医学(2) [9月5日:11:00-12:20:B]
- 蕁麻疹の謎を解いた一行の方程式 / ○李 聖林 (広島大学理学部数学科・JSTさきがけ), 秀 道広 (広島大学医学部皮膚科), 高萩 俊輔 (広島大学医学部皮膚科), 柳瀬 雄輝 (広島大学医学部皮膚科) [概要]
蕁麻疹は膨疹や限局性の浮腫が病的に出没する疾患として定義され、多くは痒みを伴う皮膚病の一つである。蕁麻疹は、ありふれた疾患でありながらその病態には複雑性や未知の部分が多く、治療に困難を極める場合もある。本研究では、極めて限られた臨床データと患者の定性的な病状データから数理モデルを構築し、医学的に全く考えられなかった蕁麻疹の仕組みを提示、皮膚医学における数理モデルの新たな可能性について議論する。
- MCC Polar Cytoskeleton’s Self-organization Simulations using Active Hydrodynamics in a Hexagonal Cell with PCP boundary conditions / ○FRANCO-MEDRANO Fermin (阪大院医学系研究科), 鈴木 貴 (阪大MMDS), 小西 聡史 (阪大院医学系研究科), 矢野 智樹 (阪大院医学系研究科), 月田 早智子 (阪大院医学系研究科) [概要]
Multiciliated Cells' (MCCs) cytoskeleton, in particular microtubules, tend to align in a series of grids and stripes, passing through several stages. MCC’s ciliar basal bodies (BBs) tend position themselves following the alignment of the cytoskeleton. Moreover, the BBs' tend to orient their basal feet (BF) towards the cytoskeleton bundles at an angle. In order to model the alignment and orientation of BBs we first model the alignment stages of the cytoskeleton. Real cells have a changing irregular shape, approximately hexagonal. So far, other existing simulations do not account for the cell shape, difficult to handle by the method of Finite Differences. The Finite Element Method is suitable to handle different shapes and fine emerging structures in the solutions. We propose a model for the cytoskeleton dynamics using Active Hydrodynamics Equations with a polarity field and solve it using the FreeFEM++ language for simulation. The simulations results show agreement on the timescales of the alignment process observed in experimental results.
- [特別講演:40分] Chemotaxis model in the immunology / ○Hyung Ju Hwang (Pohang University of Science and Technology) [概要]
In this talk, we discuss how chemotaxis affects immune system by proposing a minimal mathematical model, a reaction-diffusin-advection system, describing a cross-talk between antigens and immune cells via chemokines.
We analyze stability and instability arising in our chemotaxis model and find their conditions for different chemotactic strengths and numerical simulations are also performed to the model.
From the analytical and numerical results for our model, we explain not only the effective attraction of immune cells toward the site of infection, but also hypersensitivity when chemotactic strength is greater than some threshold.
▷ [研究部会 OS] 数理政治学 [9月4日:09:00-10:20:C]
- 協力行動に対するクラスタリングの効果 / ○守田 智 (静岡大学工学部) [概要]
利己的な行動により高い利得が生じる囚人のジレンマ的な状況で協力行動が進化・保持されるメカニズムの一つとして空間的互恵主義が知られている.そこでは,近接したプレイヤー同士間でのみゲームが行われることで互恵主義が生じる.本研究ではシンプルなモデルを用いて社会ネットワークのクラスタリング構造が協力行動の維持にどのような影響を与えるかを明らかにする.
- 二重比例法による議席配分のシミュレーション分析 / ○諸星 穂積 (政策研究大学院大学) [概要]
二重比例法(biproportional method)は,選挙区の定員と政党への議席配分が決まったとき,各選挙区での当選者を獲得投票数にできるだけ比例して決める方法である.
過去の衆議院議員総選挙のデータにこの手法をあてはめ,議席配分の偏り具合などを分析してみた結果を報告する.
- 選挙キャンペーンの決定と有権者の教育水準に関する因果関係の測定について / ○中川 訓範 (静岡大学) [概要]
本研究では、政党が行なう選挙キャンペーンと有権者の教育水準の因果関係について、政党がキャンペーンの対象とする有権者層の選択をする状況を考え、均衡で有権者層の教育水準が政党の選択に及ぼす影響を構造的に理解する理論モデルの提示し、そのモデルから導かれる因果関係の推定を推定する実証的な試みについて、その結果を報告する。
- 議席配分方式の偏りについて / ○一森 哲男 (大阪工業大学) [概要]
ウェブスター方式は平均的に偏りのない議席配分方式と主張されているが,その妥当性について考察する.最初にこれを主張したのはウィルコックスであり,その後,バリンスキーとヤングによりそれが強調された.しかし,彼らの議論を再考してみると,矛盾する点や奇妙な仮定が見られ,その結果には疑問が浮かぶ.
▷ [研究部会 OS] 数理設計(1) [9月3日:09:30-10:50:F](座長:代田 健二(愛知県立大学))
- ◎熱弾性場の3次元形状最適化解析 / ○小森 太陽 (岐阜工業高等専門学校専攻科学生), 片峯 英次 (岐阜工業高等専門学校機械工学科) [概要]
3次元熱弾性場の形状最適化問題を取りあげて,その解法を紹介する.Gmshと呼ばれるGUIソフトを利用して解析モデル,有限要素モデルを作成し,Freefem++に基づいて解析を行う解法について講演する.形状最適化手法には,分布系の形状修正感度を利用する力法を用いる.
- Shape optimization for a linear elastic fish robot / Azegami Hideyuki, ○Chancharoen Wares (Nagoya University) [概要]
This paper presents an approach to design a fish-like linear elastic
body which vibration mode becomes a swimming function. To determine the
shape, a shape optimization problem is formulated using the squared
error norm between the solution of a frequency response function problem
and the swimming function as the objective cost function and solved by
an iteration algorithm based on the 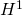 gradient method. The body is
excited by a body force located around the antinode of the swimming
function. The frequency is set as the natural frequency of the eigenmode
mostly according to the swimming function.
gradient method. The body is
excited by a body force located around the antinode of the swimming
function. The frequency is set as the natural frequency of the eigenmode
mostly according to the swimming function.
- ◎An Improved Shape Optimization Formulation of the Bernoulli Problem by Tracking the Neumann Data / Azegami Hideyuki, ○Rabago Julius Fergy [概要]
We propose a new shape optimization formulation of the Bernoulli problem by tracking the Neumann data. The associated state problem is an equivalent formulation of the Bernoulli problem with a Robin condition. We devise an iterative procedure based on a Lagrangian-like approach to numerically solve the minimization problem. The proposed scheme involves the knowledge of the shape gradient which is established through the minimax formulation. We illustrate the feasibility of the proposed method and highlight its advantage over the classical setting of tracking the Neumann data through several numerical examples.
- ◎Enhanced Collaborative Optimization Using Alternating Direction Method of Multipliers / Tao Siyu (Northwestern University), ○Shintani Kohei (Northwestern University), Yang Guang (Toyota Motor North America), Meingast Herb (Toyota Motor North America), Chen Wei (Northwestern University) [概要]
Enhanced collaborative optimization (ECO) is a recently developed multidisciplinary design optimization method in the family of collaborative optimization. While ECO achieves better optimization performance than its predecessors, its formulation is much more complex and incurs higher computation and communication costs, mainly due to the use of linear models of nonlocal constraints. Consequently, ECO is often not the most desirable method for large-scale and/or highly coupled applications. In this paper, we propose a new method named “ECO-ADMM” by introducing the alternating direction method of multipliers (ADMM) to ECO. With the aid of Lagrangian multipliers, ECO-ADMM increases each discipline’s “awareness” of global constraint conditions and search history at a negligible cost of Lagrangian multipliers updating. With case studies of two analytic test problems and an industrial vehicle suspension design problem, advantages of ECO-ADMM over ECO are observed. ECO-ADMM achieves faster convergence and better solutions than ECO in most cases where both methods have comparable settings.
▷ [研究部会 OS] 数理設計(2) [9月3日:11:00-12:20:F](座長:片峯 英次(岐阜工業高等専門学校))
- トポロジー最適化理論に基づく剛性最大化構造に対する数値的・実験的検証 / ○吉原 健太 (長岡技術科学大学 機械創造工学専攻), 倉橋 貴彦 (長岡技術科学大学 機械創造工学専攻), 小林 正成 (オイレス工業株式会社) [概要]
本研究では,トポロジー最適化理論に基づき引張り試験に対する剛性最大化構造[1]を算定し,3Dプリンタにより試験片を作成し,引張り試験を行う.初期構造の場合と比較をし,材料の低減割合に関する考察を行う.
- (講演取り下げ)
- ◎波動型方程式の係数同定逆問題に対するH1-H2勾配法 / ○倉敷 大輔 (愛知県立大学大学院情報科学研究科), 代田 健二 (愛知県立大学情報科学部) [概要]
本発表では,鉄とコンクリートによる合成梁の欠陥同定問題を例に,係数同定逆問題に対する数値解法を提案する.本研究で対象とする問題は,二つの梁を接合している連結部材のせん断方向および軸方向の劣化を同定する接触部剛性係数同定逆問題である.その係数同定逆問題を数値的に解く方法として,密度型位相最適化問題に対して有効な手法として知られる H1 勾配法と,それを元に開発された H2 勾配法を組み合わせた解法を提案する.さらに数値実験により,本提案手法の有効性を検証する.
- スカラー波動方程式の係数同定問題に対するH2勾配法 / ○代田 健二 (愛知県立大学情報科学部) [概要]
本講演では,スカラー波動方程式の係数同定問題に対する数値的再構成法について考察する.本研究で対象とする問題は,領域内部で観測された関数値から体積弾性率を表す係数関数を同定する逆問題である.その逆問題を密度型問題へと変換し,さらに 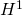 勾配法を基礎として開発された
勾配法を基礎として開発された 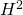 勾配法を適用することで,数値同定アルゴリズムを導出する.また数値実験により,本手法の有効性を検証する.
勾配法を適用することで,数値同定アルゴリズムを導出する.また数値実験により,本手法の有効性を検証する.
▷ [研究部会 OS] 数理的技法による情報セキュリティ(1) [9月5日:09:30-10:50:E]
- [招待講演:40分] ProVerifを用いたTLS1.3ハンドシェイクプロトコルの形式検証 / ○荒井 研一 (長崎大学大学院工学研究科), 岡崎 裕之 (信州大学大学院理工学系研究科), 布田 裕一 (東京工科大学コンピュータサイエンス学部) [概要]
ProVerifはBlanchetらが開発した形式モデル(Dolev-Yaoモデル)での暗号プロトコルの安全性自動検証ツールである.TLS 1.3はIETFにおいて2014年より標準化の議論が進められており,2018年3月にdraft-28が標準規格として承認された.講演者らは,これまでにProVerifを用いてTLS 1.3ハンドシェイクプロトコルを形式的に記述し,その安全性検証をdraft-06から継続的に行ってきた.本講演では,講演者らのこれまでの取り組みを紹介する.
- ProVerifの検証過程の可視化 / ○吉田 真紀 (情報通信研究機構) [概要]
本研究では,一般にブラックボックスである安全性検証ツールの検証過程を可視化することで検証結果の理解に貢献することを目的とする.本稿では,安全性検証ツールとして ProVerif 1.92を対象とし,検証過程で生成される情報(以降,内部情報)の抽出と可視化の手法を提案する.内部情報の抽出では,処理の順序や論理的構造を木構造として表現し,可視化では,ソフトウェアのバージョン管理の可視化に使われるツールを応用してアニメーションとして表示する.そして,代表的な暗号プロトコルの検証過程を可視化した結果を示す.
- Scyther toolの検証過程の可視化 / ○吉田 真紀 (情報通信研究機構) [概要]
本研究では,一般にブラックボックスである安全性検証ツールの検証過程を可視化することで検証結果の理解に貢献することを目的とする.本稿では,安全性検証ツールとして Scyther tool v1.1.3を対象とし,検証過程で生成される情報(以降,内部情報)の抽出と可視化の手法を提案する.内部情報の抽出では,処理の順序や論理的構造を木構造として表現し,可視化では,ソフトウェアのバージョン管理の可視化に使われるツールを応用してアニメーションとして表示する.そして,代表的な暗号プロトコルの検証過程を可視化した結果を示す.
▷ [研究部会 OS] 数理的技法による情報セキュリティ(2) [9月5日:11:00-12:20:E]
- [招待講演:40分] 同種写像暗号の数理 / ○高島 克幸 (三菱電機) [概要]
量子計算機の出現に備えて、量子計算機でも効率的に破れない公開鍵暗号の研究が活発に行われている。本講演では、その候補である同種写像暗号について概説する。同種写像の計算法、同種写像問題の困難性、そして同種写像を使った暗号系とその安全性などに関して紹介する。また、同種写像がなすグラフには、ラマヌジャングラフや火山型グラフが現れて、それらは、数理的に興味深いだけでなく、同種写像暗号を理解する上でも重要である。その紹介と共に、関連する私の研究成果についても触れる予定である。
- ◎Groebner基底を用いた同種写像核計算 / ○髙橋 康 (九州大学大学院数理学府), 安田 雅哉 (九州大学IMI研究所) [概要]
超特異楕円曲線間の同種写像核計算問題(CSSI, Computational SuperSingular Isogeny 問題)に対しては現在,量子計算機でも指数時間の攻撃法しか知られていない.そのため,CSSI問題を安全性の根拠とする暗号方式である同種写像暗号は,耐量子暗号の一つとして期待されている.本稿では,CSSI問題に対するGroebner基底計算を用いた新しい求解方法を提案する.さらに,Jaoらの提案した同種写像暗号(SIKE)に対して,提案したCSSI問題求解法を用いた解読実験結果を報告する.
- ◎DeepLLLの改良とBKZへの組込みの提案 / ○中邑 聡史 (九州大学大学院数理学府), 安田 雅哉 (九州大学IMI研究所) [概要]
格子暗号の安全性を支える最短ベクトル問題(SVP)の求解法として,
LLLやBKZなどが代表的である.LLLの自然拡張であるDeepLLLを
BKZに組込んだ“DEEP-BKZ”によるSVPチャレンジ記録更新が
SCIS2018で報告された.本稿では, DeepLLLの簡約条件を強めた
改良DeepLLLとそれをBKZに組込んだ”改良DEEP-BKZ”を提案する.
また, 出力格子ベクトルの最小ノルムと実行時間について, 既存方式と
今回の提案方式を比較し,提案手法の有効性を検証する.
▷ [研究部会 OS] 数理ファイナンス(1) [9月4日:10:30-11:30:C]
- コピュラを用いた VaR の推定について / ○Molina Barreto Andres Mauricio (中央大学商学研究科), 石村 直之 (中央大学商学部) [概要]
VaR はリスク管理において中心的な役割をなす指標の一つである。一方 copula は,確率変数の間の非線形な相関を表すのに有用な手法と認識されている。この講演では,実際の金融データを用いて VaR の copula を利用した計算手法を考察する。
- 最大値に依存する金融商品のリスク計算について / ○中津 智則 (芝浦工業大学) [概要]
株価モデルを確率微分方程式の解とした時、その解の最大値に依存する金融商品(例えばLookback optionやBarrier option)のリスク計算は非常に重要な問題である。この問題はGobet and Kohatsu-Higa(Electron. Commun. Probab., 2003)によってデルタとガンマと呼ばれるリスクが、Nakatsu(J. Comput. Finance, 2017)によってベガと呼ばれるリスクがそれぞれ考察されている。本講演では、それらの論文で扱われていたモデルよりも一般のモデルで同様の問題を考察する。
- ◎A Study on Ruin Probability of a Mortgage Loan with Risk Factors / 赤堀 次郎 (立命館大学理工学部数理科学科), Constantinescu Corina (University of Liverpool), ○今村 悠里 (東京理科大学経営学部ビジネスエコノミクス学科) [概要]
地震により家を失った者は新たにローンを組み,住家を購入する.この多重債務問題のひとつの解決策として,被害地震を受けた債務者に対してその後のローン返済を免除するモデルを提案する.本講演ではローンの破産確率が満たす多重積分方程式を与え,方程式の解が存在することを示す.また,地震の発生間隔と損害額が指数分布に従うとき,破産確率は不完全ガンマ分布に従うことを与える.
▷ [研究部会 OS] 数理ファイナンス(2) [9月5日:09:30-10:50:C]
- ◎Hyperbolic symmetrization of Heston type diffusion / ○井田 有紀 (立命館大学), 木下 剛 (立命館大学) [概要]
本講演では、双曲空間上でのReflection principleに関して得られた結果を述べる。
確率ボラティリティモデルの下でのバリアオプションのプライシングに応用を目的としている。
本研究は今村悠里氏らが行ったユークリッド空間上でのプットコールシンメトリーの研究に基づく。
- 一次元におけるバリア・オプション型期待値の計算方法について / ○浅野 了 (東京工業大学 理学院 数学系 二宮研究室) [概要]
Time changeと強Markov性を組み合わせることで、資産価格過程が一次元の場合におけるバリア・オプションの価格の別表現を求める。この表現を用いて、バリア・オプションの価格の近似が一次元ブラウン運動の弱近似とペイオフの弱近似のふたつの問題に分解できることを示す。例として、バリア・オプションに対する楠岡近似の応用を紹介する。
- 二回積分型カーネル関数を用いた偏微分方程式の数値解法について / ○家田 雅志 (みずほ第一フィナンシャルテクノロジー株式会社) [概要]
偏微分方程式の数値解法としてカーネル関数、特に動径基底関数(RBF)の線型結合を用いるメッシュフリー法がよく知られている。本講演では数理ファイナンスで現れる偏微分方程式に対して、その二階微分をRBFで近似する方法を提案し、微分係数の近似精度や境界条件が与えられていない場合の振る舞いについて議論する。
- 日本のクレジット市場における信用サイクルの変動要因 / ○廣中 純 (野村アセットマネジメント(株)) [概要]
本研究では, 市場で観測可能な要因のほか, 市場で観測できない要因(frailty)を考慮した信用イベント(格上げ・格下げ・デフォルト)の発生強度を表すモデルを提案する. また提案したモデルにより, 日本のクレジット市場における信用サイクルの変動要因の説明を試みる.
▷ [研究部会 OS] 数理ファイナンス(3) [9月5日:11:00-12:20:C]
- Risk-sensitive asset management with lognormal interest rates / ○畑 宏明 (静岡大学教育学部) [概要]
本講演では、対数正規金利過程を用いたリスク鋭感的ポートフォリオ最適化問題を扱う。この問題は標準的なリスク鋭感的確率制御問題に定式化される。
動的計画アプローチを用いて、Hamilton-Jacobi-Bellman方程式を導出し、この方程式の明示解を得る。さらに、この明示解を用いて、最適戦略を構成し最適値を得る。
- Bitcoinにおけるマイニング業者の収益に関するモデリング / ○安田 和弘 (法政大学) [概要]
FinTechの1つとしてBitcoinおよびブロックチェーン技術がある。そのBitcoinの取引情報のブロックを作るのにマイニングが行われていて、そのマイニングをし、Bitcoinを支えているマイニング業者がある。ここでは、マイニング業者の収益のモデル化を損保数理や数理ファイナンスのアプローチで考え、性質を調べていく。
- 連続制御と確率インパルス制御の混合問題に対する数値計算アルゴリズムの数値実験を通じた比較 / ○内藤 瞭介 (法政大学大学院理工学研究科), 安田 和弘 (法政大学) [概要]
第14回日本応用数理学会研究部会連合会で連続制御と確率インパルス制御の混合制御問題に対する数値計算アルゴリズムの提案を行った.そのアルゴリズムは,確率インパルス制御問題に対するFeng and Muthuraman [2010]の数値計算アルゴリズムを拡張したものであった.本講演では,既存の混合制御問題に対する数値計算アルゴリズムと提案したアルゴリズムの数値実験を通じた比較を行う.
- 二項モデル下における Predictable Forward Performance Processes を用いた期待効用に関する数値的考察 / ○佐藤 大地 (法政大学大学院理工学研究科), 安田 和弘 (法政大学) [概要]
本講演では、Angoshtari, Zarihopoulou and Zhou [2018]で考えられているpredictable forward performance processesを用いた最適投資戦略について数値的に考察をする。predictable forward performance processesでは、従来の満期まで一貫した市場での期待効用最大化に対する投資戦略ではなく、各時刻においてそのときの状況を加味した投資戦略を考える。ここでは、従来の最適投資戦略とpredictable forward performance processesを用いた投資戦略の比較をいくつかの数値実験を通して行う。
▷ [研究部会 OS] 数理ファイナンス(4) [9月5日:13:30-14:10:C]
- 1次元拡散過程を用いたペアトレーディングモデルでの最適閾値について / ○関根 順 (大阪大学大学院基礎工学研究科), 深澤 正彰 (大阪大学大学院基礎工学研究科), 前田 ひとみ (大阪大学大学院基礎工学研究科) [概要]
The static optimization problem to determine the optimal preset thresholds for pairs trading is studied in a general one-dimensional ergodic diffusion model of a stochastic spread process. An explicit formula for the
expected value of a certain first passage time is shown, and the simple equation to determine the optimal thresholds is given.
- An expansion of BSDE to study arbitrage free price of xVA. / ○田中 章博 (大阪大学大学院基礎工学研究科) [概要]
デリバティブの評価において、信用評価調整(CVA,DVA)に加えて各種コストを加味し評価を調整することが市場慣行になりつつあり、実務において段階的に対応が進められている。一方、調達コスト、信用リスク、担保交換を考慮したデリバティブの無裁定価格に関する先行研究(M.Bichuch、A. Capponi、A. Sturm)がある。本発表では、先行研究で定義されたBSDEを展開することで、実務において進められている段階的な対応と無裁定価格の関係について紹介する。
▷ [研究部会 OS] 数論アルゴリズムとその応用(1) [9月5日:13:30-14:50:E]
- ◎Coppersmithアルゴリズムを用いたNemecらによる素因数分解法について / ○菊地 修 (首都大学東京大学院修士2年), 内山 成憲 (首都大学東京教授) [概要]
昨年Nemecらは、Infineon Technologiesが製造したICカードで使用されているRSA暗号の秘密鍵の構造を解析し、その法である合成数を素因数分解する方法を提案した。この方法では、合同方程式の絶対値が小さい整数解を求めるCoppersmithアルゴリズムが使用されている。ここでは、上記の素因数分解法を実装し、その効果について考察を与える。
- 多項式x^2+5x+5に関する 2次 Frobenius 擬素数について / ○長島 早紀 (首都大学東京大学院), 篠原 直行 (情報通信研究機構), 内山 成憲 (首都大学東京) [概要]
2次 Frobenius テストは確率的な素数判定法であるため,合成数であっても素数であると誤った判定を出力する場合がある.そのような合成数は 2次 Frobenius 擬素数と呼ばれる.現在,5 を法として 2 または 3 と合同な合成数で,さらに x^2+5x+5に関する 2次 Frobenius 擬素数であるものは知られていない.ここではそのような擬素数の全体をfpsp2(-5,5) とあらわし,さらにその中で二つの素数の積である合成数の全体fpsp2_2(-5,5) と書く.
篠原は fpsp2_2(-5,5) を探索するアルゴリズムについて考察し,素数 pで,5 を法として 1 または 4と合同 かつ p < 10^9 なるものはfpsp2_2(-5,5) に含まれる合成数の素因子になりえないことを数値実験により示した.
本講演では,fpsp2_2(-5,5) に含まれる合成数の素因子について,同様の条件下で数値実験を用いて考察した結果について述べる.
- F4-style アルゴリズムの実装について / ○緑川 輝 (首都大学東京大学院修士2年), 篠原 直行 (情報通信研究機構 主任研究員), 内山 成憲 (首都大学東京教授) [概要]
耐量子計算機暗号は量子計算機が実用化されても安全性を保てると期待される暗号であり,
その代表的なものとして多変数公開鍵暗号が挙げられる.
多変数公開鍵暗号は与えられた多変数連立方程式が解かれると解読されてしまう.
その安全性を調べるために,MQChallengeというコンテストが行われており,6種の2次の多変数連立方程式が与えられている.
F4-style のアルゴリズムによるグレブナー基底の計算等によってそれらを解く研究が進められている.
本講演ではそのような多変数連立方程式に対する
F4-style のアルゴリズムの改良及び検証について発表する.
- Q(sqrt{-23})に虚数乗法を持つ楕円曲線を用いた特別な整数に対する素数証明アルゴリズム / ○小貫 啓史 (首都大学東京) [概要]
自然数nであってn-1あるいはn+1の素因数分解がわかっているものに対しては一般の自然数よりもより高速に素数証明ができることが古くから知られている。この類似として虚数乗法を持つ楕円曲線を用いることで虚二次体上の整数xでx-1の素イデアル分解が特定の形をしたものに対して素元証明を行う方法がある。今までに提案されてきたそれらの方法はすべて類数が1か2の虚二次体に虚数乗法を持つ楕円曲線を用いたものだった。本講演ではこの方法の類数が3以上の場合への拡張について述べる。特に類数が3である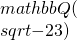 に虚数乗法を持つ楕円曲線を用いた特別な整数に対する素数証明アルゴリズムについて説明する。
に虚数乗法を持つ楕円曲線を用いた特別な整数に対する素数証明アルゴリズムについて説明する。
▷ [研究部会 OS] 数論アルゴリズムとその応用(2) [9月5日:15:00-16:20:E]
- An HFE-based variant of a key exchange protocol employing multivariate polynomial maps / ○中村 周平 (日本大学生産工学部), 伊藤 勝 (日本大学理工学部), 秋山 浩一郎 (東芝研究開発センター), 平田 典子 (日本大学理工学部) [概要]
We propose an HFE-based variant of a key exchange protocol using multivariate polynomial maps. We provide a security proof against attacks by passive observers, relying on the hardness in solving a certain system of Diophantine equations. In particular, we analyze the protocol whose underlying structure consists of HFE-based polynomial maps.
- Circulant UOV/Rainbow の安全性について / ○橋本 康史 (琉球大学) [概要]
UOV と Rainbow は多変数の2次多項式を用いた署名方式である.構成のシンプルさとその安全性から,十分実用的であると考えられており,実際にNISTのPost-Quantum Cryptography 標準化プロジェクトにおいて,提案された方式のうちいくつかは UOV と Rainbow を基にして構成されている.
Circulant UOV と Circulant Rainbow は,Peng と Tang によってごく最近提案された UOV と Rainbow を基にした署名方式である.係数に特殊な構造を入れることで,署名生成の計算量が大幅に減る一方で,既存のUOVやRainbowに対する攻撃法に対しても十分な安全性が保たれると考えられている.しかしながら,これらの方式で用いられる多項式の構造を詳しく調べると,実はKipnis-Shamir の攻撃に対して安全でないことがわかった.本講演では,これらの方式の脆弱性を説明する.
- ◎Superspecial Trigonal Curves of Genus 5 / ○工藤 桃成 (神戸市立工業高等専門学校), 原下 秀士 (横浜国立大学) [概要]
超特別曲線は代数曲線の中でも特に重要な研究対象であり,代数曲線やアーベル多様体全体を調べる手がかりとなるだけでなく,符号理論などへの応用可能性をも併せ持つ.
ここで代数曲線が超特別であるとは,そのヤコビ多様体が超特異楕円曲線の直積に同型となることである.
本講演では,種数5の「trigonal」な代数曲線において,超特別曲線を数え上げるアルゴリズムを与える.
講演者はそのアルゴリズムをMAGMA上で実行することで,標数7以下の有限体上,および標数11,13の素体上でのtrigonalな超特別曲線を全て決定し,具体的な方程式を与えることに成功した.
時間があれば,得られた超特別曲線の特徴付けや,超楕円曲線の場合における結果も紹介する.
▷ [研究部会 OS] CAEモデリングとデータ活用 [9月4日:10:30-11:45:A]
- [15分]流体構造連成解析のためのメッシュ制御技術の開発 / ○山田 知典 (東京大学) [概要]
界面追跡法による流体構造連成(Fluid-Structure Interaction, FSI)解析では,構造側の大変動に伴い流体側のメッシュのゆがみが発生し、これに起因した解析の破綻が大きな問題となっている.本研究ではFSI解析の安定性向上のため,合理的なメッシュ制御技術の開発に向けた検討を行う.
- [15分]き裂進展予測サロゲートモデルの構築 / ○和田 義孝 (近畿大学) [概要]
複数の物理法則が重畳するき裂進展をディープニューラルネットワークで学習し工学的に許容できる代替モデル(サロゲートモデル)が構築できるかどうかを検討する。重合メッシュ法を用いて2次元き裂進展解析を行い学習データを多数準備する。そのデータを用いて学習していない初期状態からき裂進展が再現できるか評価する。これまでの結果からは50万回を超える学習が必要なことが示された。効果的な学習アルゴリズムの組み合わせおよび学習させるデータセットの組み合わせを評価し工学における回帰問題への適用可能性を議論する。
- [15分]粒子法による流体解析のための粒子・ポリゴン境界表現の開発 / ○室谷 浩平 (鉄道総合技術研究所) [概要]
「固体壁を固体壁ポリゴンのみで計算する方法」は、固体壁粒子が不要になり、本来計算に必要とされる流体粒子のみ計算すればよくなる。そのため、計算コストが大幅に低くなるメリットがあるが、複雑な形状の固体壁では、固体壁を計算するアルゴリズムが複雑になるデメリットがある。本研究では、「固体壁に固体壁粒子と固体壁ポリゴンを併用する方法」を用いることにより、精度良く、低計算コストで、単純なアルゴリズムで計算することができる方法を提案する。
- [15分]Bezier曲線を生成元としたVoronoi図の正確な隣接関係の決定 / ○辻野 弘章 (和歌山大学大学院システム工学研究科), 今井 敏行 (和歌山大学システム工学部) [概要]
本研究では,Bezier曲線を生成元としたVoronoi図(勢力圏分割)の各勢力圏の正確な隣接関係を,生成元の点列近似を用いることで求める.近似算法であるため,計量情報の正しさは無視するが,位相情報すなわち隣接関係の正確性は保証する.
- [15分]視体積交差メッシュの接続性計算 / ○森口 昌樹 (明治大学 先端数理科学インスティテュート) [概要]
視体積交差法とは複数のシルエット(形状の輪郭を表す2次元図形)から3次元形状を構築するための基本的手法で,シルエットを逆投影して得られるボリュームの交差形状を抽出するものである.本研究では,Reebグラフと類似した概念を利用することで,交差形状の接続性を効率的に計算する手法を提案する.
▷ [研究部会 OS] 離散システム(1) [9月4日:09:00-10:20:E](座長:宮本 裕一郎(上智大学))
- 船速最適化を実現する船舶スケジューリングに対する高速な列生成アルゴリズム / 田中 未来 (統計数理研究所), ○小林 和博 (東京理科大学) [概要]
燃料消費量の最小化を実現するための船舶スケジューリングを扱う.そのために,各船舶が処理する貨物の順番と,運航ルートにおける港間の船速を同時に求める方法を与える.問題全体を集合分割問題して定式化するが,その制約行列の列を動的に生成する.列を生成する際に,計算時間を短縮するためのアルゴリズムを提案する.
- ◎束上の DR-劣モジュラ性による部分空間選択 / ○中島 蒼 (東京大学,理研AIP), 前原 貴憲 (理研AIP) [概要]
部分空間選択は,目的関数を最大化する部分空間を何らかの制約の下で探す最適化問題である.この問題は,主成分分析や疎辞書選択といった機械学習の重要な例を含んでいる.部分空間選択は一般には難しいが,先に挙げた二例のようにしばしば貪欲法で解けることが知られている.本研究では,なぜこれらの問題は貪欲法で解けるのか,またこのような性質はどのような目的関数と制約のクラスで成り立つのかに興味を持った.この疑問に答えるため,部分空間選択を束上の最適化問題として定式化し, directional DR-劣モジュラという新しい関数クラスを導入した.directional DR-劣モジュラ関数は,主成分分析・疎辞書選択やそれらの一般化を具体例として含んでいる.そして,directional DR-劣モジュラ関数は,種々の制約の下で貪欲法で近似比保証付きの最大化ができることを証明した.
- ◎展開型マッチングゲームにおける部分ゲーム完全均衡 / 河瀬 康志 (東京工業大学), 山口 勇太郎 (大阪大学), ○横井 優 (国立情報学研究所) [概要]
本研究では,求人者と求職者の間のマッチング市場を,展開型ゲームとして定式化する.具体的には,逐次的にジョブオファーを受ける求職者が,競合相手の戦略を考慮しながら自身の戦略を決定する状況を扱う.均衡戦略の計算複雑度についての特徴付けを与え,また,各求職者が均衡戦略に従った際に結果として得られるマッチングの性質を解析する.
- 非可換な変数をもつ多項式行列の行列式の次数の計算について / ○平井 広志 (東京大学大学院情報理工学系研究科) [概要]
本講演では,多項式行列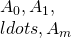 と互いに非可換な変数
と互いに非可換な変数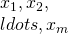 によって,
によって,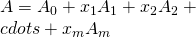 と表せる行列
と表せる行列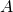 のDieudonne行列式の次数の計算について論じる.この問題は,非可換ランク計算の一般化であり,重み付き線形マトロイド交差など基本的な組合せ最適化問題を含んでいる.
のDieudonne行列式の次数の計算について論じる.この問題は,非可換ランク計算の一般化であり,重み付き線形マトロイド交差など基本的な組合せ最適化問題を含んでいる.
▷ [研究部会 OS] 離散システム(2) [9月4日:10:30-11:50:E](座長:宮本 裕一郎(上智大学))
- ◎On a construction of Ramanujan graphs / ○佐竹 翔平 (神戸大学 大学院システム情報学研究科) [概要]
Ramanujanグラフは, ある程度の「連結性」の高さが保証され, 一方で辺数が頂点数に比べ大きくならない正則グラフです. このグラフは実際のネットワークで求められる条件を満たすよいグラフとしてLubotzky, Phillips, Sarnakによって提案されました. その構成は一つの重要な問題ですが, 先行結果の多くは純粋数学の非初等的な結果に依存していました. 本講演では, 比較的初等的なRamanujanグラフの構成についてお話しします.
- ◎完全多部四点木システムからの系統樹構築 / 平井 広志 (東京大学), ○岩政 勇仁 (東京大学) [概要]
生物の進化の過程を表現する系統樹を,その部分構造(四点木)から復元する問題は,一般には NP 困難である.本研究では,「完全多部四点木システム」という四点木の集合から系統樹を復元する多項式時間アルゴリズムを構築した.
- 最小スパナー問題の困難性と固定パラメータ容易性 / ○小林 佑輔 (京都大学) [概要]
正整数 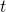 に対し, グラフ
に対し, グラフ 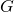 の部分グラフ
の部分グラフ 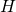 が
が 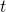 -スパナーであるとは,任意の2頂点間の
-スパナーであるとは,任意の2頂点間の 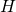 における距離が,
における距離が,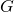 における距離の高々
における距離の高々 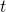 倍で抑えられていることをいう.本講演では,与えられたグラフの中で最小辺数の
倍で抑えられていることをいう.本講演では,与えられたグラフの中で最小辺数の 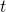 -スパナーを見つける問題を扱い,そのNP困難性と固定パラメータ容易性について議論する.
-スパナーを見つける問題を扱い,そのNP困難性と固定パラメータ容易性について議論する.
▷ [研究部会 OS] 連続体力学の数理(1) [9月5日:09:30-10:50:A](座長:木村 正人(金沢大学))
- 制限された空間での弾性薄膜の破壊 / ○赤堀 裕介 (横浜国大環境情報研究院), 増田 千紘 (横浜国大理工学部), 田中 良巳 (横浜国大環境情報研究院) [概要]
ポリマーフィルムなどの弾性薄膜を2枚の剛体板の間の狭い空間に閉じ込めて引き裂く状況を研究する。実験的には,皺パターンの形成ー薄膜の面外変形が板で拘束されることによるーや引き裂き力の著しい増大といった効果がみられる。この系に関するより詳細な実験解析と数値的検討について報告する。
- Maxwell 型と Zener 型の粘弾性き裂進展モデルについて / ○高石 武史 (武蔵野大学), 西浦 廉政 (東北大学AIMR), Avalos Edgar (東北大学AIMR), Xie Shuangquan (東北大学AIMR), 赤木 和人 (東北大学AIMR) [概要]
高石と木村によって提案されたフェーズフィールドを用いたき裂進展モデルは,バネとダッシュポットの組み合わせで考える粘弾性体のモデルにおいて,バネ部分のみからなる弾性エネルギーとフェーズフィールドを用いたき裂表面エネルギーの組み合わせを考えることで,材料の変位,き裂の有無を表すフェーズフィールド,ダッシュポット部分の歪の時間発展からなる粘弾性体のき裂進展モデルが導き出せる.既に報告したMaxwell型のみではなく,より現実の材料に近いZener型を考えることで,き裂進展にどのような影響が出るかをシミュレーション結果から解析した.
- ◎MREのための3次元粘弾性方程式に対するマルチスケール係数同定法 / ○前川 秀 (京都大学) [概要]
本講演では,MREの実現のために,time harmonicな粘弾性方程式の係数同定逆問題の数値計算手法について論じる.本研究では,この問題を適当なコスト汎関数の最小化問題として定式化する.この最小化問題に対して,共役勾配法や準Newton法などの既存の最小化手法では十分な結果が得られなかった.本講演では,この問題に対してマルチスケール係数同定法を提案し,その有効性を数値計算により示す.
- 共通ヌルクラインに基づく地震の最終滑り量の予測不能性 / ○鈴木 岳人 (青学大理工) [概要]
動的震源過程を熱・流体圧・空隙生成の間の相互作用の観点から二変数でモデル化すると、共通のヌルクラインが現れ、そこをアトラクタとする解軌道ではその最終値が初期値に敏感に依存することが分かった。物理的には初期流体圧分布が最終滑り量に強く影響を及ぼすことになる。流体圧の値は正確な測定が不可能であることから、滑り量の予測も困難であることが導かれる。
▷ [研究部会 OS] 連続体力学の数理(2) [9月5日:11:00-12:20:A](座長:平野 史朗(立命館大学))
- ◎動弾性境界積分方程式法のalmost O(N)法 / ○佐藤 大祐 (東京大学), 安藤 亮輔 (東京大学) [概要]
境界積分方程式法を動弾性問題へ適用する際、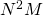 に比例して増える、積分方程式の計算量と積分核格納メモリが問題となる(ここで
に比例して増える、積分方程式の計算量と積分核格納メモリが問題となる(ここで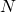 は要素数、
は要素数、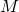 は時間ステップ数)。これらはNlogN(almost O(N))にまで削減可能とされてきた(Ergin, 1999)一方、摂動計算が必要な従来手法を数十行に及ぶ複雑な積分核(たとえばTada, 2006)へ適用することは実質的に困難だった。本講演で我々は、階層型行列法(Hackbusch, 1999)と高速領域分割法(Ando, 2016)を用い、従来法に代わる数値的なalmost O(N)法を提案する。
は時間ステップ数)。これらはNlogN(almost O(N))にまで削減可能とされてきた(Ergin, 1999)一方、摂動計算が必要な従来手法を数十行に及ぶ複雑な積分核(たとえばTada, 2006)へ適用することは実質的に困難だった。本講演で我々は、階層型行列法(Hackbusch, 1999)と高速領域分割法(Ando, 2016)を用い、従来法に代わる数値的なalmost O(N)法を提案する。
- 境界要素法における重心要素を用いないCalderonの前処理に関する一考察 / ○新納 和樹 (京都大学), 大塚 悠貴 (京都大学), 西村 直志 (京都大学) [概要]
境界要素法に対する代表的な前処理手法であるCalderonの前処理では、滑らかさの異なる積分作用素の合成積を計算する性質上、離散化において重心要素を用いたメッシュの再分割といった計算コストの高い方法を避けられないことが多い。本研究ではLaplace方程式を例にとり、メッシュの再分割を行わないCalderonの前処理について考察する。
- 波動方程式のtransmission問題における時間域境界積分法の安定性について / 三澤 亮太 (京都大学工学研究科), 福原 美桜 (京都大学情報学研究科), 新納 和樹 (京都大学情報学研究科), ○西村 直志 (京都大学情報学研究科) [概要]
2次元波動方程式のtransmission問題における時間域境界積分法の直接法において,種々のポテンシャルを適切に組み合わせると,選点法を用いた数値計算においても高い安定性が実現できることを櫻井杉浦法を用いた固有値計算によって示し,数値実験によって検証した.
▷ [研究部会 OS] 連続体力学の数理(3) [9月5日:13:30-14:30:A](座長:高石 武史(武蔵野大学))
- 筋肉における確率的挙動を示す分子モータと連続体の力学的連成の数理について / ○鷲尾 巧 (東京大学) [概要]
筋収縮はサルコメアと呼ばれる長さ2µm程度の構成単位の中に含まれる太いフィラメントと細いフィラメント間の滑り運動により実現されている。この滑り運動は熱揺らぎのもとで確率的に動作する分子モーターの10nm程度のパワーストローク運動の繰り返しによる。本講演では、分子モーターのパワーストローク運動と、サルコメアの運動、引いてはよりマクロな連続体としての筋肉の運動を結び付ける計算手法とそこから得られた心拍動の効率化に結び付く分子モーターの特性について議論する。
- ◎圧力Poisson問題と対応するStokes問題の境界条件 / ○松井 一徳 (金沢大学 自然科学研究科 数物科学専攻) [概要]
MAC法や射影法,粒子法などの非圧縮粘性流体に対する数値計算解法では,圧力を計算する技法として非圧縮性の代わりに圧力Poisson方程式が用いられている.圧力Poisson方程式を解くためには適当な境界条件を課す必要があり,本来の問題の方程式からすると多過ぎる境界条件が課されることとなる.本講演では,定常Stokes問題を用いてこの問題について調べた結果を数値計算例と合わせて述べる.
- ◎剪断流における不変解の高レイノルズ数漸近展開解析 / ○出口 健悟 (モナシュ大学) [概要]
近年、剪断流への力学系的アプローチが盛んに行われている。鍵となったのはNavier-Stokes方程式の不変解(固定点や周期軌道)の数値計算法の確立である。あるクラスの不変解の構造は、時間積分から得られる複雑な流れ場に比べいくらか単純であり、高レイノルズ数極限における接合漸近展開解析が可能である。このような不変解の漸近展開解析は、乱流等で見られる複雑な渦構造の素過程を、最小の仮定を用いて第一原理から導くことのできる有力な手段であると考えられる。
▷ [一般講演] 最適化 [9月3日:13:30-14:50:F](座長:曽我部 知広(名古屋大学))
- 情報伝達長を考慮したピラミッド組織構造の2階層リエゾン配置モデル / ○澤田 清 (流通科学大学) [概要]
本研究は,ピラミッド組織構造の2階層にリエゾンを配置し各階層の全メンバーと関係を追加するとき,リエゾンを配置する最適な2階層を求めることを目的とする.ここでは,リエゾンと組織内メンバーとの情報伝達長が組織内メンバー間の情報伝達長とは異なるモデルを提案し,組織全体の情報伝達効率を最大にするリエゾン配置の2階層を求めるための定式化を行う.
- ◎非二部的 Dulmage-Mendelsohn 分解と Berge 双対の束構造 / ○喜多 奈々緒 (東京理科大学) [概要]
本発表では二部グラフに対する古典的な成果である Dulmage-Mendelsohn(DM)分解を一般のグラフを対象にするものへと一般化し,さらにこれを用いることで極大バリアの特徴付けを与える.二部グラフのDM分解とは因子理論の基礎をなす一連の成果である標準分解の一つであり,これは線形計算やマトロイド理論への貢献においても名高い.本研究で与えるDM分解の一般化はこれまで関連性が不明であった既知の標準分解たち全てを統一的に理解する枠組みを提供する.
- ◎幾何学的最適化に基づく対称性をもつ連続時間線形システムの新しい同定法 / ○佐藤 寛之 (京都大学), 佐藤 一宏 (北見工業大学), Damm Tobias (University of Kaiserslautern) [概要]
対称性を備えた連続時間線形システムの同定は,電気回路網やマルチエージェントシステムなど,多くのシステムのモデル化において重要である.本講演では,対応する離散時間システムの同定問題をリーマン多様体上の最適化問題として定式化することで,新たな同定法を提案する.特に,既存手法により得られた近似解を初期点として幾何学的な共役勾配法を適用することで,効果的な同定が可能となることを数値実験により示す.
▷ [一般講演] 数理モデリング(1) [9月3日:16:30-17:50:A](座長:杉山 雄規(名古屋大学))
- 排除体積効果を伴う2体相互作用におけるパターン形成について / ○由良 文孝 (公立はこだて未来大学システム情報科学部), 田久保 直子 (東京大学アイソトープ総合センター), 林 達也 (東京大学大学院数理科学研究科), 間田 潤 (日本大学生産工学部), 栗原 裕基 (東京大学大学院医学系研究科), 時弘 哲治 (東京大学大学院数理科学研究科) [概要]
講演者らはこれまで、血管新生を記述する数理モデルを1次元において考察してきた。本講演では内皮細胞運動のタイムラプス撮影により推定された2次元面内での数理モデルと、そこで形成されるパターンと挙動を紹介する。新生血管に見られる樹状伸長に類似したパターンへの、細胞形状に由来する排除体積の影響を報告する。
- 拡散効果を取り入れた病原体・免疫モデルの漸近挙動 / ○佐々木 徹 (岡山大環境生命科学研究科) [概要]
病原体と免疫の相互作用の基本モデルに空間拡散の効果を取り入れたモデルの漸近挙動を考察する.このモデルは三つの平衡点を持ち,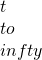 の時に解は,基本再生産数の大きさに応じた平衡点に収束する.
の時に解は,基本再生産数の大きさに応じた平衡点に収束する.
- ◎BZ反応振動子系への大域的フィードバック制御 / ○大野 航太 (明治大学大学院先端数理科学研究科), 小川 知之 (明治大学総合数理学部), 末松 信彦 (明治大学総合数理学部) [概要]
生理学や生態学、化学反応など幅広い分野で現れる自己組織化に伴うパターンダイナミクスは、反応拡散系を元とする理論で明かされてきたが、振動場で見られる多種多様なパターンを制御することは可能であるのか。我々は振動する化学反応として知られるBZ反応に、大域的な feedback 制御を導入した系を考察した。本発表では結合振動子系に縮約した系について、数理モデルと化学実験との比較結果を紹介する予定である。
- 周期昆虫における生活環恒常性の進化 / ○今 隆助 (宮崎大学) [概要]
周期ゼミのような周期昆虫の寿命の長さは,環境に依らず一定に固定されている.このように寿命を一定に保つことが,保たないことと比較して,生存競争において有利になりうることは自明ではない.本研究では,捕食者飽和が寿命を一定に保つことを,競争において有利にしうることを,数理モデルを用いて示す.
▷ [一般講演] 数理モデリング(2) [9月4日:09:00-10:20:A](座長:堀之内 成明(豊田中央研究所))
- ◎非独立なマーケット・マイクロストラクチャ・ノイズを考慮した実現ボラティリティの状態空間モデル / 石渡 哲哉 (芝浦工業大学システム理工学部), ○谷野 徹 (芝浦工業大学理工学研究科) [概要]
実現ボラティリティ(以下, RV)は, 1分毎の株価のような高頻度データから計算される株価変動率の推定量で, 近年注目を集めている. しかし高頻度データにはマーケット・マイクロストラクチャ・ノイズ (以下, MN)と呼ばれる観測誤差が入り, RVもこの影響を受ける. 本講演では, 過去と株価に依存する非独立なMNを仮定し, RVに含まれるMNによるバイアスの時系列モデリングを行う.
- 再生核補間を用いた後退確率微分方程式の数値解析 / ○田中 俊介 [概要]
後退確率微分方程式という未来の状態が条件として与えられている微分方程式があり、近年ファイナンスでは重要なツールになっています。後退確率微分方程式の近似解には決定的なものはなく研究の余地がある状況で、今回はその後退確率微分方程式の近似解を再生核補間という関数近似を用いて求める手法を提案します。
- バーゼル III 適格 Additional Tier1 債券(AT1 債)に 対する構造型プライシングモデルの改良と実証分析 / ○杉山 泰平 (三井住友アセットマネジメント株式会社), 中川 秀敏 (一橋大学大学院経営管理研究科) [概要]
バーゼル III 適格 Additional Tier 1債券(AT1 債)は,普通社債に比して高水準のクーポンが設 定されている一方,Tier1 資本を補完する「AT1 資本」として規制自己資本に算入できるという資 本性を担保するために,様々な契約条件が付されている.そのため投資家は,発行体のデフォルト (債務不履行)リスクに加えて,AT1 債が有する各種契約条件を考慮した上でプライシングをおこなうことが求められる.本論文では,先行研究を拡張して二種類の強制元本削減トリガー条項(「財務 トリガー(Accounting Trigger)」および「PONV トリガー(Point Of Non-Viability Trigger)」) を考慮した AT1 債プライシングモデルを設定し,実際に発行されている AT1 債の市場価格データ を用いた実証分析の概要を通じて,提案するプライシングモデルの有用性について検討することを 主眼とする.
- Inequality of Realization of a Stochastic Economic Dynamics based on the Erd˝os Discrepancy Problem / ○加藤 寛之 (嘉悦大学) [概要]
This paper proposes a stochastic dynamics in which people who are endowed with different discount factors buy the capital stock periodically and are exposed to randomness at arithmetic progression times. We prove that the realization of the stochastic equilibrium may render the people quite unequal benefits. Its proof is based on Erd\\H{o}s Discrepancy Problem that an arithmetic progression sum of any sign sequence goes to infinity, which is recently solved by Terence Tao (2016). The result in this paper implies that in some cases, the sources of inequality come from pure luck.
▷ [一般講演] 常微分方程式 [9月3日:16:30-17:50:B](座長:小藤 俊幸(南山大学))
- 結晶方位差と三重点による結晶粒界の発展方程式 / Epshteyn Yekaterina (The University of Utah), Liu Chun (Illinois Institute of Technology), ○水野 将司 (日本大学理工学部) [概要]
結晶はその結晶一つ一つに結晶の方位が定められており, その結晶方位のずれ, 特異性が結晶粒界でおきている. 従って, 隣り合う結晶の結晶方位差は, 結晶粒界エネルギーを考えたときに考慮に入れるべき状態変数であるが, 今まで結晶方位差はエネルギーに寄与しない仮定をおいて数学解析が進められてきた. そこで, 結晶粒界エネルギーの消散性を基礎として, 結晶方位差, 三重点の影響を考慮した新しい発展方程式を導出する.
- 非線形連立ODEとコネクトーム / ○伊藤 利明 (同志社大学) [概要]
脳における神経回路網上の電気信号の動的な振る舞いを,大規模非線形連立常微分方程式系モデルでの同期現象として扱う.この場合に神経細胞の電気信号発生に関係したODEモデルとその数値積分によるシミュレーション結果とその考察を行う.
- ◎船体転覆モデルに対するリアプノフスペクトルを用いた解析手法の検討 / ○日田 吉信 (東京海洋大学大学院海洋科学技術研究科), 上野 公彦 (東京海洋大学) [概要]
船体転覆現象への知見を得るため,船体横揺れを表す運動方程式の非線形性を解析することが本研究の目的である.今回は特に,非線形項を持つ強制ダフィング方程式を転覆方程式とした.このモデルの持つ非線形性をカオス解析で知られるリアプノフスペクトルを用いて解析した.さらに,リアプノフスペクトルを基に,初期値平面及び制御平面のカラーマップを作成したことで,非転覆領域中に特異なパターンを確認するに至った.このパターンについて,いくつか検証を行った.
- ある遅延微分方程式の陽的な周期解について / ○中田 行彦 (島根大学) [概要]
本発表では、ある非線形な遅延微分方程式(分散型の時間遅れをもつHutchinson-Wright方程式)が、平衡点が不安定な場合、周期2の周期的解をもつことを示す。Kaplan and Yorke(1974)のアイデアに倣って、ある可積分な二階の常微分方程式から、ヤコビの楕円関数で表される陽的な周期解を構成した。関連する感染症モデルに関する結果にも言及する。
▷ [一般講演] 高性能計算 [9月5日:09:30-10:50:F](座長:深谷 猛(北海道大学))
- ◎データ同化のためのアジョイント法の性能モデル構築の試み / ○藤川 隼人 (名古屋大学大学院 情報学研究科), 片桐 孝洋 (名古屋大学 情報基盤センター), 永井 亨 (名古屋大学 情報基盤センター), 荻野 正雄 (名古屋大学 情報基盤センター) [概要]
データ同化のアルゴリズムとしてアジョイント法が知られている.この計算に時空間ブロッキングを施すことで高性能化する実装方式が提案されている.本研究の目標は,この実装方式の性能モデル化手法を確立することである.時空間ブロッキングを適用したアジョイント法全体の性能モデル化を最終目標とするが,予備実験としてアジョイント法の計算の一部であるforward modelに対する空間ブロッキングの性能モデルを提案し,性能評価を行った.
- ◎OpenMPの対象ループとスレッド数を変更する自動チューニング手法の評価 / ○櫻井 刀麻 (名古屋大学大学院情報学研究科), 片桐 孝洋 (名古屋大学情報基盤センター), 永井 亨 (名古屋大学情報基盤センター), 荻野 正雄 (名古屋大学情報基盤センター) [概要]
本研究では,OpenMPの対象ループを変える自動チューニング手法の提案を行い,その有効性を検証する.名古屋大学設置のFX100を利用し,核融合シミュレーションコードGKVに対して,提案手法による自動チューニングを適用し速度向上を得た.また,自動チューニング対象の場所を実行毎に適するスレッド数に実行時に切り替える,新しい自動チューニング手法を提案し,FX100を利用して予備評価を行った.
- 医用画像処理に用いられる大変形微分同相写像のMPI並列化とコード最適化 / 中島 大地 (名古屋大学大学院 情報学研究科情報システム学専攻), 田村 友輝 (名古屋工業大学大学院 情報工学専攻), 物部 峻太郎 (名古屋工業大学大学院 情報工学専攻), ○片桐 孝洋 (名古屋大学 情報基盤センター), 本谷 秀堅 (名古屋工業大学大学院 情報工学専攻), 永井 亨 (名古屋大学 情報基盤センター), 荻野 正雄 (名古屋大学 情報基盤センター) [概要]
医療画像処理では、3次元画像を扱うためデータ容量と計算量が多い。典型的な処理として、大変形微分同相写像(Large Deformation Diffeomorphic Metric Mapping, LDDMM)の計算がある。本研究では、LDDMMの並列化を行うことで実行時間の劇的な短縮を目指す。並列化ではMPI (Message Passing Interface) を用いる。コード最適化では、ループ融合手法を用いて単体性能の向上を行った。性能評価環境として名古屋大学設置のFX100スーパコンピュータシステムを用いて、提案する実装方式の性能評価を行った。
- 有限要素解析由来の疎行列に対するFPGAを用いた線形ソルバのハードウェア化 / ○井原 遊 (東京大学大学院新領域創成科学研究科人間環境学専攻), 橋本 学 (東京大学大学院新領域創成科学研究科人間環境学専攻), 奥田 洋司 (東京大学大学院新領域創成科学研究科人間環境学専攻) [概要]
線形ソルバは数々の数値解析における計算負荷の大半を要する部分である。反復解法を用いた線形ソルバでは、疎行列ベクトル積の部分が最も負荷の高い部分であるが、計算強度が低くメモリ帯域に律速され、CPUの能力を十分に活用することが困難である。FPGAは、任意に演算装置を配置することができ、適切なバランスで設計できる。FPGAをアクセラレータとして用いることで消費電力も含め最適な計算機として活用する方法を提案する。
▷ [一般講演] 数値解析・数値計算(1) [9月5日:11:00-12:20:F](座長:剱持 智哉(名古屋大学))
- 無誤差変換技法を用いた陽的補外法の精度改善 / ○幸谷 智紀 (静岡理工科大学) [概要]
一般にBulirsch-Stoer法と呼ばれる陽的補外法は,調和数列を補助数列として使用すると丸め誤差を拡大する傾向があることが知られている。室伏・永坂らは,陽的補外法に対してMøller法を用いた精度改善法を提案しているが,今回我々が提案する無誤差変換技法を用いた方法は,計算量が増えるものの,精度改善の程度はMøller法より優れている。本講演では本技法の精度改善の検証をベンチマークテストを通じて行う。
- Enclosing the Hermitian positive definite solution of the conjugate discrete-time algebraic Riccati equation / ○Miyajima Shinya (Iwate University) [概要]
A fast iterative algorithm is proposed for numerically computing an interval matrix containing the Hermitian positive definite solution to the conjugate discrete-time algebraic Riccati equation. Numerical results show effectiveness and robustness of the algorithm.
- 新しいタイプの2 次と3 次IMEX RK公式 / ○大野 博 (茨城大学工学部) [概要]
偏微分方程式を数値解法で解く際、空間方向に離散化し、時間に関する常微分方程式に変形できる。Implicit-Explicit Runge-Kutta methods (IMEX RK 法)は、この形の常微分方程式を数値的に解くために適している。偏微分方程式を空間方向に離散化した部分を陰的方法で解き、
それ以外の部分を陽的方法で解くようにしたものである。IMEX RK 法の陽的部分の段数を増やすと、A-安定なIMEX RK 法の絶対安定領域を大きくすることを確かめた。2段と3段のA-安定なIMEX RK 法では、2つの自由パラメータが出てくる。これらのパラメ―タを高精度になるように決定する。数値例を使って、確かめたものを示す。
- シミュレーションプログラムの微分可能化と自動微分したプログラムの動作確認 / ○堀端 康善 (法政大学 理工学部) [概要]
大気シミュレーションプログラムの微分不能箇所を補間を利用して改善する。次に,自動微分ツールを使い,プログラムを微分する。内積テストを実施し,生成されたタンジェントプログラムとアジョイントプログラムの動作を確認する。
▷ [一般講演] 数値解析・数値計算(2)(〜18:10) [9月5日:16:30-18:10:F](座長:代田 健二(愛知県立大学))
- ◎べき型の非線形性を持つ確率微分方程式の爆発解の数値解析 / 石渡 哲哉 (芝浦工業大学 システム理工学部), ○梁 英哲 (芝浦工業大学大学院 理工学研究科) [概要]
本研究は, 爆発解をもつ1次元の伊藤型確率微分方程式に対するものである. 一部の確率微分方程式の爆発問題は, ブラウン運動がある特定の値へ到達する時刻を求める問題に帰着する事ができるという事がわかった. この値を用いて, 標本毎に確率的に変動する爆発時刻を不変な値で特徴付けすることができる. また, この値を数値的に推定するために既存の数値計算法の改良を試みている。
- ドロネー分割と階層的クラスタリングに基づくサッカートラッキングデータの解析 / 成塚 拓真 (中央大学理工学部), ○山崎 義弘 (早稲田大学理工学術院) [概要]
対戦型スポーツの一つであるサッカーにおけるフォーメーション形成に着目し、各選手の位置を追跡したデータ(トラッキングデータ)に対してドロネー分割および階層的クラスタリングを用いて解析した結果を報告する。
- 構造情報処理の厳密性を保証する近似図形処理フレームワーク / ○今井 敏行 (和歌山大学システム工学部) [概要]
図形処理を構造に関する情報処理に特化することで,近似アルゴリズムで厳密性を保証できることを示す.この図形処理フレームワークで,厳密性を確保したまま,アルゴリズム構築の容易性と比較的な高速性を確保できる.
- IMEX RK法の絶対安定領域の描画法 / ○大野 博 (茨城大学工学部) [概要]
偏微分方程式を数値解法で解く際、空間方向に離散化すると、時間に関する常微分方程式に変換できる。Implicit-Explicit Runge-Kutta methods(IMEX RK 法)は、このような常微分方程式の数値解法である。偏微分方程式を空間方向に離散化した部分を陰的解法で解き、それ以外の部分を陽的解法で解く方法である。IMEX RK 法の絶対安定領域は、ラフな方法で描いている。4段までのIMEX RK 法では、MathematicaのNSolveコマンドを使うと、以前よりは正確な絶対安定領域を描けることを確かめた。5段以上のIMEX RK 法の絶対安定領域を描く方法を提案する。
- ◎感染症数理モデルにおける確率最適制御 / ○加藤 京士 (東京工業大学数理計算科学系) [概要]
世界では未だ発展途上国を中心に結核、マラリアなどが流行し、また日本でもインフルエンザが毎年問題となっている。このような感染症を確率論を用いた数理モデルとして表し考えていく。本研究では大きく分けて二つの事を行った。
まず一つ目に、実データをもとに数理モデルにおけるパラメータ推定を行った。よく知られるモーメント法を一般化した手法を用いて数値計算を行い、最適なパラメータを導出した。
次に、感染症を流行させないためにワクチンをどのような割合で打っていくべきかを確率最適制御問題として扱った。ここでは金融分野などでしばしば用いられるHJB方程式を用いて問題を偏微分方程式の形で表し、それを再生核補間を用いて数値的に解析した。
先行研究により与えられた定理、考え方をもとに、本研究では解析的に解けていない部分を近年の数値解法に基づき扱っていく。
▷ [一般講演] 偏微分方程式(1) [9月5日:13:30-14:50:F](座長:村井 大介(豊田中央研究所))
- ◎SKT交差拡散定常極限方程式の解の多重度と安定性の数値解析 / ○森 竜樹 (阪大基礎工), 鈴木 貴 (阪大MMDS), 四ツ谷 晶二 (龍谷大理工) [概要]
1979年に重定・川崎・寺本により提案された個体群密度に依存する非線形な拡散を伴う2種競争系に現れるある定常極限問題の大域的解構造について考える.Lou-Ni-Yotsutaniらによって非定数定常解の存在・非存在, 解の形状, 解の全体構造の概要が明らかにされているが,解の一意性・多重度については予想にとどまっていた.本講演では空間1次元での定常極限問題の解の多重度と安定性について数値的に調べた結果を報告する.
- ◎非対称細胞分裂における極性パターン形成メカニズムの解明 / ○中原 智弘 (広島大学), 李 聖林 (広島大学 JSTさきがけ) [概要]
初期発生過程における非対称細胞分裂のメカニズム解明は発生生物学において重要な課題の一つである。非対称細胞分裂の初期段階に細胞は細胞膜、細胞質において自らが持つたんぱく質を左右非対称に局在させ極性パターンを形成する。本研究では空間二次元の移流反応拡散方程式系とPhase-field法を融合させ細胞の形を反映した数理モデルを構築することにより細胞膜、細胞質における極性パターン形成のメカニズムを解明する。
- ルジャンドル陪関数の変形と応用12 / ○田川 昭夫 (なし) [概要]
ルジャンドル陪関数を変形すると、
Rn.m(cosθ)*(sinθ)^mの形になる。
等速運動をする球体の軸対称の流れを、ストークス近似で解く。
Δ{rotVn}=0の解から、速度Vn、圧力Pηが決まる。
解をナビエストークス式の左辺に代入すると、
二次慣性項の造る圧力P3の代数解を得る。
ポアソン方程式の右辺に、Rp.0*Rn.0の2次積が現れる。
- 文字列の非可換位相半群上の偏微分方程式と生物群集の動態解析 / ○小谷野 仁 (東京工業大学), 澤田 和典 (株式会社ぐるなび), 山本 希 (東京工業大学), 山田 拓司 (東京工業大学) [概要]
1 つの環境中の生物群集が持つ DNA や遺伝子配列の全体は、アルファベット A = { a, c, g, t } 上の文字列の非可換位相半群 A* 上の確率関数として表される。本発表では、A* 上に 1 つの環境中の DNA 配列の集団の時間発展を表す偏微分方程式を導入し、その混合モデルにより DNA 配列の集団に掛かる淘汰圧を表すために導入された A* 上の分布の推定論を展開して、人工的に高塩環境に改変する前後の、ある植物の周辺環境中の微生物群集から収集された 16S リボソーム RNA 遺伝子配列を題材とし、配列の集団の時間発展をコンピューターの中で再現して、解析した結果を述べる。
▷ [一般講演] 偏微分方程式(2) [9月5日:15:00-16:20:F](座長:畔上 秀幸(名古屋大学))
- de Sitter時空におけるKlein-Gordon方程式の解の伝播について / ○土屋 拓也 (早稲田大学), 中村 誠 (山形大学) [概要]
宇宙的スケールにおける現象の多くは、強い重力によって引き起こされている。強い重力のもとでは時空が曲がるため、その現象を記述する発展方程式の形が平坦の場合に対して変化することが知られている。今回、宇宙が収縮していく場合の例として、de Sitter時空の収縮する場合を考え、その時空の情報がどのように方程式の解に影響を及ぼすかについて、数値計算を用いて考察する。その際、相対論的波動方程式の1つであるKlein-Gordon方程式の数値解がどのように伝播していくかについて講演する予定である。
- 非局所境界条件にむだ時間を含む双曲型システムに対する状態推定 / ○丸山 颯天 (神戸大学), 佐野 英樹 (神戸大学), 若生 将史 (神戸大学) [概要]
本講演では,非局所境界条件にむだ時間要素をもつ1階双曲型システムに対し,オブザーバ構成法を述べる.たとえば,線形化された Kermack-McKendrick モデルにおいて潜伏期間を考慮したモデルは,このクラスの双曲型方程式に含まれる.偏微分方程式に対するバックステッピング法を用いて,無限次元のオブザーバが設計できることを示す.
- Voronoi 格子上における離散 Green-Gauss 公式を介した離散変分とその応用 / ○降籏 大介 (大阪大学サイバーメディアセンター) [概要]
微分方程式の数値解析における構造保存数値解法の重要な一つのポイントは Green-Gauss 公式の離散化にある.というのも、この公式は局所的操作たる微分と大域的操作の積分をつなぎ、関数の “変分” という概念を成立させるキーとなっているからである.本講演は、Voronoi 格子上の有限差分/体積法における離散 Green-Gauss 公式が素直な性質を持っていること、その格子上で離散変分という概念 が自然に成立することを示し、そしてその応用として、離散変分導関数法という構造数値解法が成立することを示す.
- 量子システムの理論的な最適制御問題について研究 / ○王 全芳 (香港中文大学) [概要]
量子システムは放物型の系で記述される偏微分方程式なので、この講演はこれらの非線形系の最適制御問題を考える。量子システムの理論的な制御のみを取り扱うことにする。つまり、変分法の方法で、複数の関数空間で、弱解と最適解の存在性と一意性を証明するつもりです。特に、具体的な方程式の例を挙げて、これらの制御問題を解決できることを示します。物理分野と違って、応用数学の立場で、量子システムの制御問題を解くことは理論的に実現して見たいです。さらに、今までこの研究方向で得られたいくつの結果を報告させていただきたいです。
▷ [一般講演] 統計科学(〜18:10) [9月5日:16:30-18:10:A](座長:宮武 勇登(大阪大学))
- 統計多様体上の状態空間モデルを用いた発展型ネットワーク解析 / 小松 瑞果 (神戸大学), ○谷口 隆晴 (神戸大学, JST さきがけ), 大川 剛直 (神戸大学, JST CREST) [概要]
近年のセンサー・通信デバイス等の発達により,これまで取得が困難であった様々なデータが取得できるようになってきている.本研究では,そのようなデータとして,特に,ネットワークとして扱うことが適切であるものを考え,その時間発展の解析手法として,ネットワークモデルのつくる多様体上の状態空間モデルに基づく手法を提案する.
- Benfordの法則に従う分布の構成 / ○小澤 一文 (秋田県立大学名誉教授) [概要]
最近,数値の先頭桁の値の分布に関してBenfordの法則という法則が注目されている。これは,自然科学,画像処理,ビックデータの解析など,多くの分野での応用が期待される。本講演では,正確にBenfordの法則に従う分布の構成と,乱数の生成に関して議論する。
- 双対平坦空間における次元削減について / ○熊谷 敦也 (日本大学商学部) [概要]
双対平坦空間でいくつかの点が与えられたとき重心からの平均ダイバージェンスは Bregman information と呼ばれ、分散や相互情報量を一般化した情報量となる。本講演ではまず、点間のダイバージェンスを内積行列に変換し固有値分解を行うことで上記情報量に対しPCAや古典的MDSと同様の次元削減ができることを示す。またダイバージェンスと自己双対な測地線の関係について取り上げ、これを利用した次元削減について述べる。
- 強化学習による囚人のジレンマを考慮した戦略を持つマルチエージェントシステムの提案 / ○内海 友貴 (法政大学大学院), 李 磊 (法政大学理工学部) [概要]
マルチエージェントシステムにおいて単体のエージェントが合理性を求めて行動を選択してしまうことで、集団としては最適な行動を取ることができない場合がある。エージェント同士の行動の競合により作業効率の低下といった不利益を生じさせるといった例が考えられる。これは囚人のジレンマと呼ばれる問題の例であり、人間の振る舞いを模倣するエージェントが最適行動の学習をする際に考慮しなければならない問題点である。本研究では、予め戦略を持たせその後強化学習により他者を意識し集団で利益が出る最適な行動ができるマルチエージェントシステムの提案を目的とする。
- ◎サッカーのパス回しによってつくられるネットワークの成長について / ○山本 健 (琉球大学), 成塚 拓真 (中央大学) [概要]
本研究では、サッカーの試合において選手から選手へパスが通るたびに選手同士を辺で結んでできるネットワークに注目する。試合が進むほどパスが増え、ネットワークは密に成長していく。このネットワークの時間変化を説明するために、“すでに多くのパスが通った選手にパスを出しやすい”という優先的選択の性質を仮定した確率モデルを提案する。このモデルを理論的に解析し、実際のサッカーの試合のデータとの比較をおこなう。
▷ [一般講演] 流体計算 [9月5日:16:30-17:50:E](座長:片峯 英次(岐阜工業高等専門学校))
- MPS法による静水圧問題における重心ボロノイ分割を用いた粒子位置の提案 / ○長谷川 颯 (名古屋大学大学院情報学研究科情報システム学専攻), 荻野 正雄 (名古屋大学情報基盤センター), 片桐 孝洋 (名古屋大学情報基盤センター), 永井 亨 (名古屋大学情報基盤センター) [概要]
今回,MPS法の効率化として,粒子の初期位置について着目した.粒子の初期位置は格子状配置が主流であるが,それでは斜面や曲面を階段形状で表現することになり,数値計算結果の精度に悪影響を及ぼすことが知られている.そこで今回は重心ボロノイ分割を用い生成した粒子位置について静水圧問題に適用し,精度評価を行った.
- 2層渦あり流れの数値シミュレーション / ○東海林 まゆみ (日本女子大学), 岡本 久 (学習院大学) [概要]
重力波、重力・表面張力波、表面張力波の2層渦あり流れの分岐問題を考える。様々な研究がなされている渦なし流れに対して、渦あり流れに関しての研究はまだ少ない。ここでは上層と下層でそれぞれ異なる渦度(定数)の2層流を扱っている。パラメータを様々に変えたとき、分岐解の形状や分岐構造がどのように変化するか、よどみ点がどのようなしくみで出現するのか、を数値シミュレーションによって調べた。
- ◎粒子法シミュレーションのキャビテーション気泡における圧縮破壊現象への応用 / ○西 圭祐 (生体情報(数学)研究室) [概要]
近年,キャビテーション気泡によって発生する圧縮破壊現象が,工業や医療技術へ数多く応用されている.本研究では,数値解析シミュレーション手法の中でも,ラグランジュ的解析により複雑な流体の形状変化の再現に優れた粒子法を用いて,圧縮破壊現象の再現を行う.具体的には,キャビテーション気泡のマイクロジェット発生や,様々な条件下における非球状収縮の様子について,シミュレーション結果と実験結果を比較した.
- Stokes-Darcy 方程式に対する処罰法と不連続Galerkin近似 / ○周 冠宇 (東京理科大学), 柏原 崇人 (東京大学), 及川 一誠 (早稲田大学), Chung Eric (The Chinese University of Hong Kong), Shiue Ming-Cheng (National Chiao Tung University) [概要]
インタフェース境界上で連続な法線流速を持つStokes-Darcy 方程式に対する処罰法を提案し,処罰法の適当性と誤差評価を行う.さらに,不連続ガレルキン(DG)法を処罰問題に適用し,対称的DGスキームを提案する.数値スキームに関して,安定性と収束性を考察する.特に,滑らかなインタフェースを折れ線によって近似する際に生じる誤差を精査し,処罰パラメータと離散パラメータの最適な関係を導出する.
▷ [正会員主催 OS] 先進的環境における数値計算と関連HPC技術(1) [9月5日:15:00-16:20:C](座長:深谷 猛(北海道大学))
- マルチコア・メニーコア計算機環境におけるChebyshev基底通信削減CG法の性能評価 / ○大島 聡史 (九州大学), 藤井 昭宏 (工学院大学), 田中 輝雄 (工学院大学), 深谷 猛 (北海道大学), 須田 礼仁 (東京大学) [概要]
大規模並列計算機環境におけるCG法は集団通信がボトルネックとなることが指摘されている。そのため計算順序を変更して集団通信の回数を削減したり、非同期通信を活用するなど、様々な改善手法が提案されている。本研究ではChebyshev基底通信削減CG法をとりあげ、最新の計算機環境において性能評価を行った結果を紹介する。
- ◎GPUにおけるSELL形式疎行列ベクトル積の性能評価 / ○佐藤 駿一 (筑波大学大学院システム情報工学研究科), 高橋 大介 (筑波大学計算科学研究センター) [概要]
疎行列ベクトル積は科学技術計算で広く使われる計算である.
そのため,疎行列ベクトル積に関して,疎行列の格納形式を疎行列の構造に応じて変更することによる高速化は重要である.
近年アクセラレータとしてGPUが注目されており,GPUを用いた疎行列ベクトル積に関する研究が盛んに行われている.
本稿ではGPUが搭載されているシステムにおいてSELL形式の疎行列ベクトル積の実装を行い,性能評価を行った.
- ◎ディープラーニングを用いた数値計算ライブラリにおける反復解法の前処理選択の検討 / ○山田 賢也 (名古屋大学大学院情報学研究科), 片桐 孝洋 (名古屋大学情報基盤センター), 永井 亨 (名古屋大学情報基盤センター), 荻野 正雄 (名古屋大学情報基盤センター) [概要]
疎行列を対象とする数値計算ライブラリでは,実装選択に関するチューニングパラメタが多く存在するが,その設定の違いによる計算性能の差が非常に大きい.また,最適実装は計算を行う疎行列に依存する.そこで本研究では,ディープラーニングによる機械学習を行うことで最適実装を予測する手法を提案し,実験を通してその評価を行う.今回の実験では複数存在するチューニングパラメタの内,前処理選択について検証を行った.
- ◎Oakforest-PACS上におけるSA-AMG法の高並列環境下に向けたHybrid並列化に関する分析 / ○野村 直也 (東京大学), 中島 研吾 (東京大学) [概要]
メニィコアプロセッサを結合したクラスタでは, MPIとOpenMPを併用したHybrid並列プログラミングモデルが適しているとされる.そこで本研究は,連立一次方程式の解法であるSA-AMG法にHybrid並列化を行い,Oakforest-PACS(OFP)上で実行時間や並列化効率の分析を行う.OFPは,メニーコア型プロセッサであるIntel(R) Xeon Phi(TM)プロセッサによる超並列クラスタ型コンピュータシステムである.OFP上でHybrid並列を適用することで,実行時間や並列化効率の改善がみられると期待できる.
▷ [正会員主催 OS] 先進的環境における数値計算と関連HPC技術(2) [9月5日:16:30-17:50:C](座長:大島 聡史(九州大学))
- 密テンソルに対するALS法の実装方法に関する考察 / ○深谷 猛 (北海道大学) [概要]
密なテンソルのCP分解を計算する代表的な手法としてALS(Alternating Least Square)法が知られている。本発表では,ALS法を素朴に実装し,近年のマルチコアCPU環境上でその性能を評価する。処理の並列性やメモリアクセスコストなど,高性能計算の観点から実装方法を考察し,より効率的な実装に向けた検討を行う。
- 大規模な数値線形代数の問題における精度保証付き数値計算 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
本発表では,「極限の探究に資する精度保証付き数値計算学の展開と超高性能計算環境の創成」というプロジェクトにおける,芝浦工業大学グループの研究の進捗現状について報告する.数値線形代数の問題に対する精度保証付き数値計算を扱っており,特に連立一次方程式の精度保証法,PBLASを用いた区間演算,高精度計算について紹介し,理研の京コンピュータと富士通FX100などを用いた結果について紹介したい.
- タイルサイズチューニングのためのタイル QR アルゴリズムの性能モデル / ○鈴木 智博 (山梨大学), 高柳 雅俊 (山梨大学) [概要]
タイルアルゴリズムによるQR分解は4つの基本演算(カーネル)をタスクとしたタスク並列型プログラムとして実装される。実装の性能はタイルサイズに大きく依存するが、タスク間のデータ依存を監視しながら動的なタスクスケジューリングを行うので性能モデルの構築が難しい。今回、回帰分析によりカーネル単体の性能モデルを構築し、実際の行列分解プログラムにこれらを組み込むことで簡易な性能モデルを構築した。
- EigenExaへのオンライン自動チューニング活用の試みについて / ○今村 俊幸 (理化学研究所) [概要]
我々はエクサスケール規模の次世代スパコンでの実用を目指した固有値計算ライブラリEigenExaを開発している。現状、「京」など超並列環境では通信コストが並列性の阻害要件となっており、本研究においてベイズなどの統計により適切な通信方法をオンライン推定し実行時のシステムに適した通信最適化を試みる。特にATMathCoreLibを使ったソフトウェアフレームワークと構築、予備実験について講演時に報告する。
▷ [正会員主催 OS] 非線形問題のシミュレーションと可視化(1) [9月3日:09:30-10:50:C](座長:仲田 晋(立命館大学))
- ◎Modified Improved Interpolating Moving Least Squares 近似を用いた Element-free Galerkin 法の精度向上 / ○藤田 宜久 (函館工業高等専門学校), 伊東 拓 (日本大学), 生野 壮一郎 (東京工科大学), 中村 浩章 (核融合科学研究所) [概要]
メッシュレス法の一つである Element-free Galerkin (EFG) 法は内部で導関数近似を行っている.そこで,導関数近似の精度向上を目的として Modified Improved Interpolating Moving Least Squares (MIIMLS) 近似を開発した.MIIMLS近似をEFG法へ組み込んだ結果,解析精度はMLS近似を用いた計算より向上していることを確認した.
- 微小スケール領域における電磁波伝搬解析へのメッシュレス法の適用 / ○伊東 拓 (日本大学), 藤田 宜久 (函館工業高等専門学校), 生野 壮一郎 (東京工科大学), 中村 浩章 (核融合科学研究所,名古屋大学) [概要]
本研究の目的は,微小スケール領域における電磁波伝搬シミュレーションを行う際にメッシュレス法を適用し,その安定性について調査することである.そのために,近接場光学顕微鏡におけるプローブでの電磁波伝搬シミュレーションを考え,長時間安定的に実行するための条件について検討する.
- メッシュレス法を用いた電磁波伝搬シミュレーション / ○齋藤 歩 (山形大学大学院理工学研究科), 高山 彰優 (山形大学大学院理工学研究科), 神谷 淳 (山形大学大学院理工学研究科) [概要]
電磁波伝搬シミュレーションには,有限差分時間領域(FDTD)法が広く使われている.しかしながら,FDTD法は一般に陽解法であるため,定常状態になるまでに多大なタイムステップを要してしまう.本講演では,メッシュレス法を用いた定常電磁波伝搬問題の数値解法を開発し,同法の性能を数値的に評価した結果を示す.
- 溶液中における対称双頭型両親媒性分子の自己会合:散逸粒子動力学シミュレーション / ○藤原 進 (京都工芸繊維大学), 水口 朋子 (京都工芸繊維大学), 橋本 雅人 (京都工芸繊維大学) [概要]
溶液中における対称双頭型両親媒性分子の自己会合構造に及ぼす粒子間相互作用の効果を分子レベルで明らかにするため、対称双頭型両親媒性溶液の散逸粒子動力学シミュレーションを行い、ミセルやチューブ、ベシクルなどの形成過程を解析する。
▷ [正会員主催 OS] 非線形問題のシミュレーションと可視化(2) [9月3日:11:00-12:20:C](座長:齋藤 歩(山形大学))
- 通信回避アルゴリズム付き共役勾配法の収束改善 / ○松元 朗 (東京工科大学), 藤田 宜久 (函館工業高等専門学校), 伊藤 拓 (日本大学), 生野 壮一郎 (東京工科大学) [概要]
Krylov部分空間解法は並列化することが容易である一方,分散処理の数に比例して集団通信が増大してしまう難点をもつ.この難点を克服するために,通信回避アルゴリズムが提案されているが,同手法を用いると収束特性が悪化することが知られている.
本研究では,通信回避共役勾配法の収束改善について新たな手法を提案する.
- ◎ポリゴンモデルから局所的陰関数曲面モデルへの変換 / ○谷 周世 (立命館大学大学院), 仲田 晋 (立命館大学), 風間 正喜 (富士通), 諏訪 多聞 (富士通) [概要]
本講演では,多面体として表現された3次元形状のポリゴンモデルを局所的陰関数曲面モデルへ変換する手法を提案する.局所的陰関数曲面モデルは形状の表面付近のみを定義域とする関数のゼロ等値面として定義される曲面のことである.局所的陰関数曲面モデル生成には関数値の評価が速い区分的多項式による手法を採用した.そして,本手法による定義域の局所化により,少ないデータ量で高解像度の陰関数曲面モデルへの変換を可能とした.
- バーチャルリアリティ空間における核融合炉の組み立て / ○大谷 寛明 (核融合科学研究所), 宮澤 順一 (核融合科学研究所), 高丸 尚教 (中部大学), 嘉無木 昇 (中部大学), 石黒 静児 (核融合科学研究所) [概要]
核融合炉の設計では、建設時の組立工程や稼働開始後のロボットアームを含めた保守作業手順を検討する必要がある。構造物やロボットアームの動きには構造解析や機構解析が必要であり、現在、その検討を進めている。また、没入型バーチャルリアリティ(VR)装置を使ってロボットアームを含めた炉設計データを3次元VR空間に投影して、炉の部品を含めたロボットアームシステムの動きを確認できるシステムを構築した。
▷ [正会員主催 OS] 非線形問題のシミュレーションと可視化(3) [9月3日:13:30-14:50:C](座長:大谷 寛明(核融合科学研究所))
- 等価回路モデルによるHTS内の遮蔽電流密度解析 / ○山口 敬済 (山形大学), 高山 彰優 (山形大学), 齋藤 歩 (山形大学), 神谷 淳 (山形大学) [概要]
High−Temperature Superconductor (HTS)を電流ループの集合を用いて近似すれば,HTSの電磁気的性質を等価回路モデルを用いて表すことができる.同モデルから得た回路方程式を解くことによって,HTS内の遮蔽電流密度の時間発展を決定することができる.
- プラズマ対向壁リサイクリングモデル開発を目指した水素プラズマ照射の分子動力学シミュレーション / ○斎藤 誠紀 (釧路工業高等専門学校), 中村 浩章 (核融合科学研究所), 澤田 圭司 (信州大学), 小林 政弘 (核融合科学研究所), 河村 学思 (核融合科学研究所), 蓮尾 昌裕 (京都大学) [概要]
磁場閉じ込め核融合炉内の周辺領域でのプラズマ挙動理解のため、衝突輻射モデルや中性粒子輸送コードが用いられる。しかし、プラズマ対向壁において反射・放出される原子・分子の放出角や振動・回転状態の情報は乏しい。そこで本研究では、これらの情報を計算する水素プラズマ対向壁リサイクリングモデルの構築を目指し、プラズマ対向壁に水素原子を打ち込む分子動力学シミュレーションを行う。
- タングステンフラクタル構造の光学応答シミュレーション / ○中村 浩章 (核融合科学研究所), 中村 浩章 (名古屋大学), 浅野 恵吾 (名古屋大学), 安永 卓生 (九州工業大), 梶田 信 (名古屋大学), 大野 哲靖 (名古屋大学), 吉田 直亮 (九州大学) [概要]
核融合炉材料の候補材であるタングステンにヘリウムを照射するとある条件下でファズ構造と呼ばれるフラクタル構造をとることが知られている。FDTDシミュレーションを用いて、このファズ構造を簡略化したタングステンフラクタル構造に電磁波を照射し光学応答を調べた。複雑な構造になればなるほど反射率が減少することが分かった。
- 超伝導リニア駆動型ペレット入射法のFEMシミュレーション / ○高山 彰優 (山形大学), 山口 敬済 (山形大学), 齋藤 歩 (山形大学), 神谷 淳 (山形大学) [概要]
核融合炉のプラズマ中心にペレットを到達させるため,近年,高温超伝導リニア駆動型ペレット入射法が提案された.本研究の目的は,高温超伝導内遮蔽電流密度解析のための有限要素法コードを開発することである.さらに,高温超伝導リニア駆動型ペレット入射法のシミュレーションを行うことによって,同ペレット入射法の加速性能を調べることである.
▷ [正会員主催 OS] FreeFem++での開発と利用 [9月3日:15:00-16:20:F](座長:高石 武史(武蔵野大学))
- 超収束するHDG法の開発 / ○及川 一誠 (早稲田大学) [概要]
Hybridizable Discontinuous Galerkin (HDG) 法はある条件下で超収束することが知られている.本講演では,数値フラックスを未知関数とした場合についての結果を紹介する.FreeFem++を用いたHDG法の数値計算法についても述べる.
- 非定常性を考慮した熱弾性場の形状最適化 / ○片峯 英次 (岐阜工業高等専門学校), 広瀬 智史 (岐阜工業高等専門学校 専攻科学生) [概要]
非定常の熱弾性場に対して,剛性最大化を目的とする形状最適化問題を取りあげて,その解法を紹介する.問題を定式化し,随伴変数法を利用して形状修正の感度となる形状勾配密度関数を導出した.導出した感度に基づいて力法(あるいは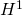 勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
- Development of Dynamic Loading Module in FreeFem++ for Obtaining a System of Linear Equations / ○藤原 宏志 (京都大学), Hecht Frédéric (University Pierre and Marie CURIE) [概要]
FreeFem++は有限要素法による微分方程式の数値計算環境を提供している.近年MPIによる並列計算にも対応したが,特に大規模な問題を並列計算などで解く際には別途の並列計算環境の利用が有効な場合がある.本発表では,そのために,FreeFem++で得られる離散問題,特に連立一次方程式をHarwell-Boeing形式で取得するためのダイナミックローディングモジュールの実装例を示す.
- 半導体ドリフト拡散方程式での指数関数重み係数の要素積分法 / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
ドリフト拡散方程式の混合型有限要素法近似では電子/正孔密度分布とその勾配の要素剛性行列は静電場に指数関数で依存する係数関数の積分が必要である. FreeFem++ が備える多項式オーダーの数値積分公式では近似精度が不足するため, 指数関数の定積分を用いる計算法を導入する.
▷ [講習会] FreeFem++での開発と利用(〜18:00) [9月3日:16:30-18:00:F](座長:高石 武史(武蔵野大学))
- 流体構造連成問題 — 弱連成形式での力の釣り合いと領域の変形 / ○高石 武史 (武蔵野大学), 鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
弱連成形式では弾性体Navier方程式と非圧縮流体Stokes方程式を力の釣り合いを考慮しながら逐次的に領域を変形させることで解を構成する. 境界での流体の応力を弾性体に反映させる方法として, 流体の近似解を直接微分して応力を計算するものと, 部分積分を通してNeumann境界を課す剛性行列と流体の近似解の積からデータを取り出すものの二種を扱う.
▷ [正会員主催 OS] 自己駆動運動の数理解析 [9月5日:15:00-16:20:A]
- ◎有限領域に閉じ込められた樟脳粒の自己駆動運動 / ○小谷野 由紀 (千葉大学), 末松 J. 信彦 (明治大学), 北畑 裕之 (千葉大学) [概要]
自己駆動粒子を有限サイズの領域に閉じ込めると、自己駆動粒子が領域境界の影響を受けて運動する場合がある。水面に浮かべた樟脳粒はその一例である。自己駆動粒子である樟脳粒は水面に界面活性をもつ樟脳分子を拡散し、表面張力勾配に駆動されて動くが、樟脳分子の濃度場は領域の境界からも影響を受けるため、樟脳粒の運動は境界の形状に依存する。本研究では、円形領域に閉じ込めた樟脳粒の運動の解析を行った。
- ◎円環水路上に現れる樟脳円板のクラスター運動に対する数学解析 / ○岡本 守 (北海道大学理学院博士課程), 後藤田 剛 (北海道大学電子科学研究所附属社会創造数学研究センター人間数理研究分野), 長山 雅晴 (北海道大学電子科学研究所附属社会創造数学研究センター人間数理研究分野) [概要]
円環水路上で樟脳円板は種々の集団運動を生じることが知られている.今回,集団運動の中でも樟脳円盤が非対称な配置のままで等速運動を行うクラスター運動に注目し,水面の樟脳分子濃度を記述した反応拡散方程式と,樟脳円板の運動方程式を組み合わせたモデル方程式を解析した.解析の結果,クラスター運動の出現には樟脳分子濃度から表面張力を表す関数の凸性が重要であるとの結論を得たので,これを報告する.
- 流体力学を伴う液滴の自発運動と相互作用 / ○義永 那津人 (東北大学WPI-AIMR, 産総研MathAM-OIL) [概要]
液滴の表面張力の勾配によって周囲の流体運動を生じる現象はマランゴニ効果と呼ばれている。液滴と流体に加えて、表面張力を変化させる化学物質の場が存在し、液滴が化学反応によってその化学物質を生成する非平衡状態において、液滴は自発的に運動し変形する。ここでは、流体方程式と反応拡散方程式を用いてこの現象を記述し、弱非線形解析によって、液滴の自発運動速度と形に関する閉じた方程式を導出する。また、二つの液滴の間に働く相互作用について議論する。
- 単一自己駆動粒子が呈する準周期的な運動の数理解析 / ○池田 幸太 (明治大), 宮路 智行 (明治大), 北畑 裕之 (千葉大), 小谷野 由紀 (千葉大), 義永 那津人 (東北大) [概要]
単一の自己駆動粒子は外力や外場との相互作用を通じて、振動、回転、準周期的な運動といった、様々な種類の運動を呈することが知られている。本研究では単一の自己駆動粒子が満たすべき数理モデルを一般的に扱う。適当な条件下で不変多様体を構成し、多様体上の低次元力学系を解析することで、準周期的な運動に相当する解が安定的に存在することを示す。
▷ [正会員主催 OS] Max-Plus代数の数理とその応用(1) [9月4日:09:00-10:20:F](座長:渡邊 芳英(同志社大学))
- [招待講演:40分] Max-Plus代数からトロピカル幾何へ,最近の進展と工程計画問題への応用 / ○小林 正典 (首都大学東京・大学院理学研究科・数理科学専攻) [概要]
Max-Plus代数に対応する新しい代数幾何学として「トロピカル幾何学」が興り,Max-Plus代数と関わる様々な分野に幾何的手法を持ち込めるようになった.対象であるトロピカル多様体には,複素多様体の極限としての類似が利く,組合せ論的考察が可能,可視化が容易,といった利点がある.本講演ではトロピカル幾何学の最近の進展と,工程計画問題への応用について述べる.
- [招待講演:40分] Max-Plus代数のダイナミクス / ○高橋 大輔 (早稲田大学基幹理工学部応用数理学科) [概要]
Max-Plus代数および関連の代数の上で定義される時間発展方程式は,非線形波動や多粒子系など運動を伴う系の離散表現として有効である.本講演では,それらのダイナミクスについて方程式と解の構造の立場から解説を行う.また,より広い立場から,Max演算が関わる時間発展系の数学についても触れる.
▷ [正会員主催 OS] Max-Plus代数の数理とその応用(2) [9月4日:10:30-11:50:F](座長:友枝 明保(武蔵野大学) )
- [招待講演:40分] 数理計画問題におけるmax-plus代数の活用 ~制御工学から組合せ最適化まで~ / ○五島 洋行 (法政大学) [概要]
Max演算および+演算をそれぞれ加算および乗算として扱うmax-plus代数は,複数事象の同期や並列動作といった制約が線形な式で記述できるため,事象駆動型システムの記述に適している。PERTの日程計画問題から,現代制御理論の知見を援用したスケジューリング問題,時間パラメータが確率的変動をする場合,組合せ最適化問題との融合など,古典的な応用から最近の話題まで,max-plus代数を用いた各種の数理計画問題への応用について述べる。
- Max-Plus代数とスケジューリング問題 / ○久保 奨 ((独)統計センター), 西成 活裕 (東京大学先端科学技術研究センター) [概要]
フローショップスケジューリング問題に対して,max-plus代数における行列を使った新たな定式化を与えた.これにより,線形代数との関係性等を用いて,見通し良く計算することが可能になった.また,メイクスパンを最小にする並列同一2機械問題の数学的構造が,max-plus代数における“代数方程式”を解くことで明らかにできることが分かった.
- ◎Max-Plus代数における行列の核とその基底の特徴づけ / ○西田 優樹 (同志社大学大学院理工学研究科数理環境科学専攻) [概要]
線形空間及びその基底はMax-Plus代数においても主要なテーマの1つであるが,Max-Plus代数における有限生成な線形空間の基底は本質的に一意的であるという通常の代数では見られない性質を持つ.本講演では線形空間として特にMax-Plus代数上の行列の核をとりあげ,Cramerの公式の類似を用いてその基底に含まれる有限なベクトルの特徴づけを行う.
▷ [正会員主催 OS] 多倍長精度浮動小数点演算の高速化手法と応用(1) [9月4日:09:00-10:20:B]
- [招待講演:40分] Intel AVX-512命令を用いた複数の整数除算の高速化 / ○高橋 大介 (筑波大学計算科学研究センター) [概要]
本論文では,Intel AVX-512命令を用いて複数の整数除算を高速化し性能評価を行った結果について述べる.
多くの64ビットプロセッサでは128ビットの被除数と64ビットの除数に対する整数除算命令がサポートされているが,同様の演算を行うSIMD命令は著者の知る限り存在していないのが現状である.
そこでAVX-512命令を用いて複数の128ビットの被除数と64ビットの除数に対する符号なし整数除算を高速化する手法を提案する.
また,AVX-512命令を搭載したXeon Phiプロセッサにおける性能評価の結果についても報告する.
- 多倍長精度浮動小数点演算の並列化 / 八木 武尊 (東京理科大学), 菱沼 利彰 (筑波大学), 石渡 恵美子 (東京理科大学), ○長谷川 秀彦 (筑波大学) [概要]
FMA (Fused Multiply and Add), AVX2 (Advanced Vector Extensions 2), OpenMP などを用いて、行列やベクトルに対する Double-double 演算や Quad-double演算を高速化する際のポイントや性能向上について述べる。疎行列-ベクトル積を高速化するためにBCRS(4, 1)を導入したDouble-double演算についても述べる。
- 4倍長精度・高次数解法による常微分方程式の数値解法 / ○平山 弘 (神奈川工科大学) [概要]
4倍精度を使い20次程度の高次のTaylor級数を使って、悪条件の常微分方程式を数値的に解いた。1913 年にC.Burrau によって研究されたピタゴラス三体問題は、1967 年にエール大学のSzebehely らによって、Levi-Civita 変換を利用して数値計算によって解決された。ここでは、4倍精度を使い、24 次のTaylor 展開法を使い、特別な変換を使わないで、高精度な計算結果を得ることができることを示す。
▷ [正会員主催 OS] 多倍長精度浮動小数点演算の高速化手法と応用(2) [9月4日:10:30-11:50:B]
- [招待講演:40分] 多倍長計算環境exflibの最新計算環境への対応と普及 / ○藤原 宏志 (京都大学大学院情報学研究科) [概要]
近年,多倍長計算が広く実装され,先端的科学・技術計算で従来は数値的不安定性のために実現困難とされていた数値計算の実現例や高精度計算例が報告されている.本研究では,この多倍長計算の実用化と普及を一層促進するため,著者が独自に開発を進める多倍長計算環境exflibのOpenMP並列計算への対応,および商用ソフトウエアMATLABへの対応について述べる.
- [招待講演:40分] PEZY-SC2上における倍々精度Rgemmの実装と評価 / ○菱沼 利彰 (株式会社PEZY Computing), 中田 真秀 (理化学研究所) [概要]
本研究では,MIMD型メニーコアプロセッサPEZY-SC2上に高精度演算ライブラリQDに実装されている倍々精度の基本演算を移植し,これらを組み合わせてRgemm (行列-行列積)を実装し,PEZY-SC2向けに最適化を行った.発表では,はじめにPEZY-SC2の構成やプログラミング方法,倍々精度ライブラリpzqdの機能について述べた上で,最適化の方法や性能について紹介する.
▷ [正会員主催 OS] 応用力学系(1) [9月3日:09:30-10:50:B](座長:國府 寛司(京大理))
- 余次元2の分岐に対する標準形の非可積分性 / Acosta-Humánez Primitivo (Simón Bolívar大学), ○矢ヶ崎 一幸 (京都大学) [概要]
余次元2の分岐は力学系における基礎的かつ興味深い現象であり,中でもfold-Hopfおよび2重Hopf分岐はとりわけ重要である.本報告では,これら2つの分岐の標準形がBogoyavlenskijの意味で非可積分であるための十分条件を与え,ほとんどすべてのパラメータの値に対して非可積分であることを証明する.特に,fold-Hopf分岐の標準形に対してはこれまでに知られていたものよりも弱い条件の下で非可積分であることが示される.この目的のため,これら標準形の非可積分性が2次元多項式ベクトル場のものに帰着できることを示し,AyoulとZungによるMorales-Ramis-Simo理論の一般化に基づく,2次元多項式ベクトル場の非可積分性に対する判定アルゴリズムを新たに提案し適用する.
- ◎2自由度ハミルトン系における横断的なヘテロクリニック軌道の存在と非可積分性 / 矢ヶ崎 一幸 (京都大学情報学研究科), ○山中 祥五 (京都大学情報学研究科) [概要]
ヘテロクリニック軌道により連結されたサドル・センター型の平衡点をもつ2自由度ハミルトン系を考え,サドル・センター近傍に存在する周期軌道に対する横断的なヘテロクリニック軌道の存在と非可積分性との関連性について論じる.また,具体例として4次ポテンシャルを有する系を取りあげ,得られた結果の有用性を確認する.
- ◎摂動系における周期軌道, ホモクリニック軌道, 第一積分および可換なベクトル場の非保存 / ○本永 翔也 (京都大学情報学研究科), 矢ヶ崎 一幸 (京都大学情報学研究科) [概要]
周期軌道あるいはホモクリニック軌道と,第一積分あるいは可換なベクトル場をもつ力学系が摂動を受けるとき,それらが微小変化を許して存在し続けるための必要条件を与える.また,周期軌道およびホモクリニック軌道が存在するための十分条件を与える標準的なメルニコフの方法との関係についても論じる.
- ◎遅延微分方程式に対する岡村の距離関数と解の一意性のための十分条件 / ○西口 純矢 (東北大学 数理科学連携研究センター) [概要]
岡村はタイムラグを持たない常微分方程式に対して,いわゆる「岡村の距離関数」を用いて一意性のための必要十分条件を与えた.本講演では,講演者による遅延微分方程式の初期値問題の統一的理論を背景として,岡村の距離関数を遅延微分方程式に拡張しその条件を与える.また,通常の Lipschitz 条件を拡張した「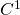 -延長に関して局所 Lipschitz」という仮定の下で,岡村の距離関数の具体例の表示を与える.
-延長に関して局所 Lipschitz」という仮定の下で,岡村の距離関数の具体例の表示を与える.
▷ [正会員主催 OS] 応用力学系(2) [9月3日:11:00-12:20:B](座長:矢ヶ崎 一幸(京大情報))
- 倒立バネ振り子モデルによるヒトの歩行・走行・転倒の分岐 / ○森田 英俊 (京都大学), 青井 伸也 (京都大学), 土屋 和雄 (京都大学), 國府 寛司 (京都大学) [概要]
ヒトの歩行・走行のモデルとして,簡単なハイブリッド力学系モデルが提案されている.歩行や走行のアトラクターとその吸引域だけでなく,転倒を示す領域も存在し,パラメータによってそれらの様相は変わる.その力学系としての機構を理解すべく,前回までに我々は,単純化した(鉛直方向)一次元運動(相空間が二次元)のハイブリッド力学系において,常にベクトル場Iにいるアトラクター(接地したままの上下運動)と,ベクトル場IとIIを行き来するアトラクター(跳躍),さらにIIからIへ戻れずに軌道が発散する振る舞い(転倒)の共存を伴う新しい分岐を発見し,その機構を解析した.今回は,これを水平方向を含む二次元に拡張したバネ振り子モデル,特に変数の内の一つを制御した相空間が三次元の力学系モデルが,実際に前方への歩行・走行の挙動を示し,さらに歩行・走行・転倒の共存を伴う分岐が見られたので報告する.
- ◎レイリー・ベナール対流におけるラグランジュ的な流体輸送の解析 / ○渡辺 昌仁 (早稲田大学大学院基幹理工学研究科機械科学専攻), 吉村 浩明 (早稲田大学基幹理工学部機械科学・航空学科) [概要]
本発表では,速度ベクトル場に摂動を加えた2次元のレイリー・ベナール対流における流体混合に関連してラグランジュ・コヒーレント構造の解析を行い,ラグランジュ的なカオス輸送の機構を明らかにする.また,ポアンカレ写像を用いて,安定な輸送領域に存在するKAMトーラス,準周期軌道及び周期解の大域的構造について述べる.
- On a novel variational approach to robust finite time optimal control / ○藤本 健治 (京都大学), 大倉 裕貴 (京都大学) [概要]
This talk presents a novel variational approach to finite time optimal control robust again parameter variation. The effect of the parameter variation to the state trajectory is modeled by the variational method. Controllability analysis of such dynamics clarifies the class of suppressable parameter variations with state trajectories. The proposed method is applied to a trajectory generation problem for a simplified oscillatory model.
- (講演取り下げ)
▷ [正会員主催 OS] 応用力学系(3) [9月3日:13:30-14:50:B](座長:吉村 浩明(早大))
- ネットワーク上の蔵本モデルの同期現象 / ○千葉 逸人 (九州大学マス・フォア・インダストリ研究所) [概要]
蔵本モデルは同期現象を記述する代表的な数理モデルである。ここでは一般のグラフの上で定義された蔵本モデルを考え、グラフの連続極限や一般化スペクトル理論を用いて、そのダイナミクスを調べる。特に、グラフの離散構造がダイナミクスにどのように影響するのかを明らかにする。
- ネットワーク力学系の同期とネットワーク構造 / ○國府 寛司 (京都大学・大学院理学研究科) [概要]
あるネットワーク構造の結合力学系の複数のコピーを結合させた力学系の同期現象について,Fiedler-望月の determining node の理論を用いて議論する.特にいわゆる Feedback Vertex Set でないノードの集合が同期のための determining node になることを示す.
- 複数のグラフに依存する結合振動子系の連続極限 / 伊原 亮輔 (京都大学), ○矢ヶ崎 一幸 (京都大学) [概要]
グラフ上の結合振動子系はニューラルネットワークやジョセフソン接合配列,電力ネットワークなど多くの数理モデルを表す.本報告では,複数のグラフに依存する結合振動子系を取りあげ,それらの連続極限についての理論結果を与える.また,具体的な適用例に対して数値シミュレーションを行い,理論結果の有効性を確認する.
- 化学反応経路網の幾何学的理解に向けて / ○荒井 迅 (中部大学創発学術院) [概要]
第一原理計算を用いた化学反応の研究が近年飛躍的に拡大しているが,得られた高次元の計算データを可視化し,その幾何学的な構造を理解する手法はまだ不十分な状況である.そこで,同変モース理論やコンレイ指数,計算トポロジー理論,さらにグラフの構造保存埋め込み理論などを用いて化学反応経路網を幾何学的に理解する取り組みを紹介する.本講演は北大の武次研究室との共同研究を含むものである.
▷ [正会員主催 OS] 応用力学系(4) [9月3日:15:00-16:20:B](座長:矢ヶ崎 一幸(京大情報))
- 三体8の字解と、それから分岐する解の線形安定性 / ○藤原 俊朗 (北里大学), 福田 宏 (北里大学), 尾崎 浩司 (東海大学) [概要]
三体8の字解は等質量平面三体問題の周期解の一つで,8の字の形をした一つの軌道の上を3質点が同じ時間間隔で互いを追う解である.粒子間のポテンシャルを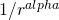 として指数
として指数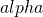 をパラメーターとして解を延長すると,いくつかの
をパラメーターとして解を延長すると,いくつかの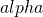 で解の分岐が生じる.
この講演では,8の字解および分岐した解の線形安定性について述べる.
で解の分岐が生じる.
この講演では,8の字解および分岐した解の線形安定性について述べる.
- ◎確率的レイリー・プレセット方程式の変分的定式化と分岐現象の解析 / ○牛奥 隆博 (早稲田大学大学院 基幹理工学研究科 機械科学専攻), 吉村 浩明 (早稲田大学 基幹理工学部 機械科学・航空学科) [概要]
単一気泡ダイナミクスのモデルであるレイリー・プレセット方程式は,周期的に変動する周辺圧力の振幅をパラメータとして周期倍分岐を起こし,カオスへと至る非線形系として知られている.本発表では,速度場に揺らぎを与えた確率的レイリー・プレセット方程式のモデルの提案とその変分的定式化を行う.その上で,加振圧力の振幅に関する確率的レイリー・プレセット方程式の分岐現象を調査し,揺らぎの影響について検討を行う.
- SU(p,q)上の自由剛体の力学系に関する安定性解析 / ○多羅間 大輔 (立命館大学理工学部数理科学科), Ratiu Tudor S. (上海交通大学数学科学学院) [概要]
MishchenkoとFomenkoによって定式化された一般化された自由剛体の完全積分可能なHamilton力学系を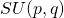 の場合に考え,平衡点の安定性を解析した結果について報告する.
の場合に考え,平衡点の安定性を解析した結果について報告する.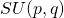 とは符号数
とは符号数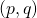 のHermite内積に関するユニタリー行列全体のなすLie群である.Lie環
のHermite内積に関するユニタリー行列全体のなすLie群である.Lie環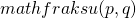 のCartan部分環ごとに可積分なHamilton力学系が
のCartan部分環ごとに可積分なHamilton力学系が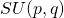 上に定まり,そこから対称性によって誘導されるLie環上のEuler方程式により力学系の挙動が記述できる.この講演では,Euler方程式の孤立平衡点の安定性を解析し,ルート系の言葉を用いるとCartan部分環ごとに安定性が決定されることを示す.時間が許せば,付随する
上に定まり,そこから対称性によって誘導されるLie環上のEuler方程式により力学系の挙動が記述できる.この講演では,Euler方程式の孤立平衡点の安定性を解析し,ルート系の言葉を用いるとCartan部分環ごとに安定性が決定されることを示す.時間が許せば,付随する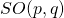 上の自由剛体についても触れる.
上の自由剛体についても触れる.
- 変分的積分法と非平衡熱力学系への応用 / ○吉村 浩明 (早稲田大学), Gay-Balmaz Francois (Ecole Normale Superieure de Paris) [概要]
正則なラグランジアンに対するハミルトンの変分原理から導かれるオイラー・ラグランジュ方程式は,接バンドル上にwell-definedなフローを自然に誘導する.特に,離散ハミルトンの原理から離散オイラー・ラグランジュ方程式を導くことができるが,この変分的積分法は離散化されたシンプレクティック構造を保存する積分法となる.本研究では,非線形かつ非ホロノミックな拘束を受ける非平衡熱力学系の変分的定式化に対して,離散的な変分公式を導き,離散化されたシンプレクティック構造を一般化した構造を保存する積分法であることを例とともに示す.
▷ [正会員主催 OS] ブロックチェーンと応用数理 [9月5日:16:30-17:50:B]
- [10分] ブロックチェーンセッションへのイントロ / ○佐古 和恵 (NEC) [概要]
数理ファイナンス、数理政治学、情報セキュリティ、産業における応用数理の各研究部会の観点からブロックチェーンの議論を行う本セッションにおいて、議論の土台となるブロックチェーンの概要を10分で紹介する。
- 政治学から見たブロックチェーン / ○岸本 一男 (筑波大学名誉教授) [概要]
政治学から見たブロックチェーン技術の可能性を検討する.
- 仮想通貨、スマートコントラクト、リスクの計量化:数理ファイナンスの立場から / ○関根 順 (大阪大学大学院基礎工学研究科) [概要]
仮想通貨を一つの”資産クラス”と見做して投資対象とする試み、ブロックチェーンを基盤技術としたスマートコントラクトの開発など「仮想通貨・ブロックチェーン」に関連した金融実務界での様々な取り組みが見られる。ICT技術的観点ではなく、「数理ファイナンス的」観点に立って今後の課題・チャレンジについて考察する。
- スケーラビリティと分散化について / ○岡本 龍明 (NTT) [概要]
ブロックチェーンや仮想通貨を公開化された形で多数の参加者が利用するときの大きな問題としてスケーラビリティがある。これは、すべてのトランザクションの承認合意を一本のブロックチェーンを用いて分散環境の下で行うときに必然的に発生する問題である。このような問題は集中管理の下では発生せず、ある意味でスケーラビリティと分散化はトレードオフの関係にあるとも言える。この問題について、現在行われている取り組みを参考に考察を行う。
▷ [正会員主催 OS] 乱数生成と評価 [9月3日:13:30-14:50:A]
- 一様分布との適合度検定を用いた乱数性判定におけるP値の分布の離散性の影響の解析 / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]
NIST 乱数検定では,得られたP値の分布と一様分布との適合度検定を用いた乱数性の判定法が提案されている.著者等は2015年度の年会でFrequency Test と Rank Testについて,P値の分布の離散性の影響で,適合度検定としてカイ二乗検定を用いる場合,対象とする系列数が多くなると真の乱数であっても設定された有意水準以上の頻度で検定に不合格となることを理論的に示した.本研究では,適合度検定にコルモゴロフ-スミルノフ検定を用いた場合について,P値の分布の離散性が判定結果へ影響することを理論的に示し,カオス真軌道,および,メルセンヌ・ツイスターによって生成した系列に対する数値実験によって結果を検証する.
- Overlapping Template matching検定におけるテンプレートの選び方に関する一考察 / ○岩崎 淳 (福岡工業大学) [概要]
NIST乱数検定ツールに含まれるOverlapping Template matching検定では,数列にテンプレートと同じパターンがあらわれる回数をもとに検定を行う.テンプレートとしては連のみが規定されている.本発表では,テンプレートを任意に拡張し,複数の検定にまたがる参照分布の結合分布を導出する方法を述べる.さらにそれを用いて,P値が独立に近い(であろう)2種類のテンプレートの選び方の一案を述べ,その例についてのP値の独立性に関する実験結果を報告する.
- ◎整数上のカオス写像におけるビット毎の0/1の出現確率に関する一考察 / ○村岡 英之 (九州工業大学), 荒木 俊輔 (九州工業大学), 宮崎 武 (北九州市立大学), 上原 聡 (北九州市立大学), 硴崎 賢一 (九州工業大学) [概要]
本稿では,整数上で定義されたテント写像やロジスティック写像等のカオス写像において,演算の過程で求まる値の二進ビット列におけるビット毎の0/1の出現確率を調査し,乱数が満たすべき等確率性の観点から,擬似乱数生成に適したビット抽出位置について議論する.
- ラグ付きフィボナッチ生成法に対するある非統計的検定について / ○原本 博史 (愛媛大学) [概要]
古くから使われているラグ付きフィボナッチ生成法は、下位桁の0,1分布が悪いことが知られており、下位桁を捨て去る改良などが行われている。本講演ではこの捨て去りがどの程度有効かを、符号理論に
現れるMacWilliams恒等式を用いて非統計的に検証した結果と、その近似計算可能性に関する実験結果を紹介する。
▷ [正会員主催 OS] クルマづくりを支える応用数理 [9月5日:15:00-16:20:B](座長:堀之内 成明(豊田中央研究所))
- [23分] 形態最適化計算の自動車関連の実問題への応用 / ○村井 大介 (株式会社 豊田中央研究所), 吉田 広顕 (株式会社 豊田中央研究所) [概要]
複数の部品を接着する際に、接着不良による不良品の発生を防ぐことは、生産コストを低減する上で重要である。本発表では、部品同士の接着状態や各種設計要件を満たす形状を、形状最適化やトポロジー最適化といった計算手法を駆使して求めた結果を紹介する。
- [19分] 車載エアコン用モータの音響シミュレーション / ○柘植 竜也 (株式会社 デンソー), 大澤 司 (株式会社 デンソー), 池田 和正 (株式会社 デンソー) [概要]
ロータ磁気音の周波数変調現象メカニズムを理論検討し、数値計算手法を使い妥当性を評価した。 さらに磁界計算-振動計算-音響計算が連成するCAE技術を構築し、ロータ磁気音の詳細メカニズムを明らかにした。
- [19分] 自動車の電動化に向けた開発・製造における熱流体シミュレーション / ○堀之内 成明 (株式会社 豊田中央研究所) [概要]
自動車の車両電動化に向け,熱流体シミュレーションは様々な広がりを見せつつあり,車両やエンジンの開発のみならず,パワー半導体の製造プロセスのような新たな分野への適用が試みられている.本稿では,それらにおける計算手法や数理モデルの取組みを紹介する.
- [19分] Deep Convolutional Neural Networkによる自動車用オートマチックトランスミッションの制御に現れる時系列データの2値分類 / ○井手 貴範 (アイシン・エィ・ダブリュ株式会社), 川上 雄史 (アイシン・エィ・ダブリュ株式会社), 富田 陽久 (アイシン・エィ・ダブリュ株式会社), 森山 英二 (アイシン・エィ・ダブリュ株式会社), 筒井 洋 (アイシン・エィ・ダブリュ株式会社), 保木 邦仁 (電気通信大学), 村松 正和 (電気通信大学) [概要]
深層学習においてよくしられている畳み込みニューラルネットワークは画像の識別問題において高精度の正答率を持つ.本公演では自動車用オートマチックトランスミッションにおける制御に現れる時系列データの2値分類に対して畳み込みニューラルネットワークを用いた手法とその数値実験結果を紹介する.
▷ キャリアデザインのためのランチミーティング [9月3日:12:30-13:30:D]
今回の年会でも,若手・女性研究者が日ごろ気になっていることを多くの方と共有し,情報交換を行う時間を設けました。今回は,若手のキャリアデザインに焦点を当てて,参加者間の情報交換・意見交換,また学会への意見・要望などをいただければと思っております。少しばかりの軽食と飲み物をご用意してお待ちしております。事前の登録等は不要ですので,お気軽にご参加ください。
-
◎座席位置選択モデルにおける状態空間生成条件について / ○小笠原 悠 (首都大学東京) [概要]
本研究では列状の座席を考えたとき,予約を座席位置に受け入れていくことで埋まっていく座席の状態空間の生成方法を考える.このような状態空間の内包表記として条件を与えることで,抑えることが出来る要素数や,実際には推移しないが生成される要素数などを示す.更に,実際には推移しない要素の生成によるRevenue Managementの収益最大化問題での再最適化上の問題を紹介する.
-
消失点検出のための直線の確率表現に基づく投票法 / ○舛本 高紀 (和歌山大学大学院システム工学研究科), 陳 謙 ((株)センスタイムジャパン), 今井 敏行 (和歌山大学システム工学部) [概要]
本研究では,確率に基づく消失点の検出手法について考察と改善を行う.直線パラメータの確率表現に基づく累積確率による投票法で消失点を検出する.この投票の際,線分上の確率を除外することで誤検出が起きないようにする.
-
◎計算手順と配列の並び替え手順の最適化によるn次元HOTRGの計算時間の削減 / ○山田 悠加 (筑波大学), 今倉 暁 (筑波大学), 今村 俊幸 (理研R-CCS), 櫻井 鉄也 (筑波大学) [概要]
本研究では、分配関数の近似計算手法の一つである高次テンソルくりこみ群(HOTRG)の高速化を行う。HOTRGのボトルネックは複数テンソルの縮約であり、計算量はテンソルの縮約手順に依存する。またテンソルの縮約は行列積により計算されるが、そのための配列の並び替えの計算時間が問題になっている。本研究ではn次元モデル向けのHOTRGの並列実装に対して、計算時間を削減する計算手順と並び替え手順を提案する。
-
◎Robust Multi-material Topology Optimization for Lattice Structure Under Material Uncertainties / ○Shintani Kohei (Northwestern University), Chan Yu-Chin (Northwestern University), Chen Wei (Northwestern University) [概要]
Recent advances in additive manufacturing have enabled the manufacture of hollow shapes with complex external geometry and multiple materials using networks of small periodic cells known as lattice structures. The porosity and high number of elements in these structures generate lightweight designs with improved performance and functionality. This paper proposes a design approach for lattice structures considering both multi-material design and uncertainty in material properties. A density-based multi-material topology optimization method is proposed to find the optimal geometry and material layout. In addition, a new interpolation scheme for using multiple and arbitrary materials is presented. For robustness of structural compliance against uncertainty in material properties, a weighted sum of the mean and standard deviation is chosen as an objective function. To estimate statistical moments by the material uncertainty, the univariate dimension-reduction (UDR) method combined with Gauss-type quadrature sampling is employed. Two numerical examples demonstrate the efficiency of the proposed approach and the effect of material uncertainty on the robust design results.
-
◎多集団年齢構造化SIR感染症モデルを用いたクラミジア疫学データの考察 / ○國谷 紀良 (神戸大学大学院システム情報学研究科) [概要]
本研究では,国内における近年の性器クラミジア感染症の疫学データに対し,多集団年齢構造化SIR感染症モデルの大域吸引性を利用して,感染症の流行強度を表す基本再生産数Roの推定を行う.その際,モデルの特殊例である単性,両性,年齢依存単性,年齢依存両性の4種類のモデルを比較する.結果として,Roは1.0148から1.0535の範囲にあり,年齢構造は性構造よりもRoの値に与える影響が大きいことが示される.
-
◎粒子法とBohm形式による波束の干渉の数値解析 / ○廣野 史明 (法政大(情報)), 岩沢 美佐子 (法政大(理工)), 善甫 康成 (法政大(情報)) [概要]
粒子法を用いて二重スリットでの干渉解析を行った。Bohm形式を用いると量子ポテンシャルとして量子効果が分かりやすい。一方、粒子法は計算点を粒子と見なして波束の運動を解析する手法である。しかし干渉を解析するには波束の拡散により計算点間の距離が広がることから精度の点で数値的に不安定になる。そこで計算点を解析中に動的に追加と削除し最小二乗法で補正することで安定に解析を継続する手法を考案した。
-
グラフの閉路リダクションを用いたMin-Plus行列の対角化 / ○佐藤 宏平 (小山高専), 西田 優樹 (同志社大学), 渡邉 扇之介 (小山高専) [概要]
一般的に,Min-Plus代数における正方行列の固有値の個数は,その行列の次数以下であることが知られている.従って,独立な固有ベクトルの個数も行列の次数以下しか存在せず,通常の線形代数に倣った固有ベクトルを用いた行列の対角化を行うことは不可能である.
本講演では,Min-Plus代数上の正方行列に対して,その行列を重み付きの隣接行列として得られる有向グラフに現れる閉路にリダクションという操作を繰り返し用いることで,行列の対角化が得られることを述べる.これにより得られる行列は対角ブロック行列であり,各ブロック行列からは行列の固有多項式の相異なる根を求めることができる.
-
◎深層学習におけるskip結合の理解 / ○長瀬 准平 (芝浦工業大学大学院理工学研究科), 石渡 哲哉 (芝浦工業大学システム理工学部) [概要]
近年、深層学習分野の研究は盛んに行われており、実社会への応用も含めて多くの関心が寄せられている。一方で、理論的な解析や体系的な議論はその需要に反して多くない。本研究では、2015年に提案されて以来重要な働きをしているResidual skipという機構について数理的に議論を行い、既存のモデルとの比較およびネットワークの構造に関する考察を行う。
-
◎グレブナー基底を用いた黄金比に収束するファジーセルオートマトンの列挙 / ○福田 亜希子 (芝浦工業大学), 渡邉 扇之介 (小山工業高等専門学校) [概要]
エレメンタリーセルオートマトン(ECA)とは時間・空間がともに離散的で2値{0,1}の状態を持つ離散力学系である。ECAにおいて状態が[0,1]の連続値をとれるように拡張したものがファジーセルオートマトン(FCA)である。本研究では,黄金比に収束するFCAをグレブナー基底によって特徴付け,列挙した。この手法を用いると,他の値に収束するFCAの列挙も可能である。
-
◎力学的境界条件下におけるCaginalp systemに対する構造保存スキーム / ○奥村 真善美 (大阪大学) [概要]
力学的境界条件を伴うCaginalp systemに対し, 離散変分導関数法によって構造保存スキームを構成した. 力学的境界条件下でのCahn-Hilliard方程式に対し, 離散変分導関数法を適用した数値計算結果はあるが, それは境界条件の近似が空間に関して非対称であった. 今回提案するスキームは問題の方程式は違うが, 境界での対称性を回復できており, 境界近傍の精度が良くなっていると期待する. また, 本スキームの構成法は前述のCahn-Hilliard方程式の場合にも適用可能であると期待している.
-
Mathematical modeling of cell-cell adhesion and its applications / ○村川 秀樹 (九州大学), Carrillo Jose A. (Imperial College London), 佐藤 純 (金沢大学), 富樫 英 (神戸大学) [概要]
細胞同士、または細胞と細胞外基質が接着する現象は細胞接着と呼ばれる。また、生体内で各細胞がその機能を発揮するために適切な場所に移動し、適切な構造を形成する現象は細胞選別と呼ばれている。これらの現象は、個体発生時の臓器形成や、成体の組織細胞における機能協調、組織の再構築に関わる非常に重要な現象として、細胞生物学や発生生物学などの分野において活発に研究がおこなわれている。その一方で、数理的観点からの研究は十分になされているとは言い難い。本ポスターでは細胞接着・細胞選別現象に関する実験結果の紹介し、それらの現象を記述する数理モデルを提出する。数値実験結果は、提案モデルが定性的にも定量的にも現象を再現するものであることを示唆している。本ポスターでは、更に、生命科学における現実問題の解明に向けた応用についての研究成果を報告する。
-
折紙工法による紙/樹脂製緩衝材兼運搬箱の開発 / 萩原 一郎 (明治大学), 寺田 耕輔 (奈良高専), ○阿部 綾 (明治大学) [概要]
折紙工学研究の一環として、緩衝材としてハニカムボードに代わる箱入りアッセンブリトラスコアパネル(Box in Assembly Truss Core Panel: BATCP)が開発された。本研究ではBATCPに緩衝材としての役割と運搬箱の両方の役割を持たせることを考える。運搬対象物はそれぞれに極力避けたい周波数帯域があるため、問題となる周波数帯域で伝達特性を低くする方法について検討したものを紹介する。
-
◎Einstein方程式の補正形式と重力崩壊の数値計算 / ○浦川 遼介 (早稲田大学), 土屋 拓也 (早稲田大学), 米田 元 (早稲田大学) [概要]
Einstein方程式は強重力場中では数値計算が破綻しやすく,適切な定式化が必要である。そのような定式化の1つに補正形式があり,拘束伝播方程式の係数行列の固有値(CAF)を調べることにより安定性が議論できる。本発表では,重力崩壊を題材に,物質場がある場合でもCAFの議論が有効であることを数値計算によって示す。
-
(講演取り下げ)
-
◎コウイカにおける動的パターン形成メカニズムの理解に向けて / ○水野 佳奈 (島根大学総合理工学研究科), 岩本 真裕子 (島根大学総合理工学研究科) [概要]
コウイカの体表パターンは瞬間的に変化し、チューリングパターンに比べて時間スケールが速い。本研究では、コウイカの動的パターン形成メカニズムの理解を目指し、コウイカにおける体表の構造を元にバネ質点系のシンプルなモデルを構築した。本発表では数理モデルの概要とその数値シミュレーション結果について議論する。
-
粘着円充填 / ○牧田 渉 (龍谷大学), 岸田 健太 ((株)イーオン), 須志田 隆道 (北海道大学), 山岸 義和 (龍谷大学) [概要]
シリンダー 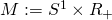 で、半径
で、半径 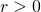 の円板
の円板 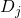 (
(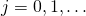 ) を上から落として積み上げていく。ただし
) を上から落として積み上げていく。ただし 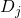 の中心を
の中心を 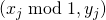 とすると、
とすると、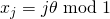 であり、
であり、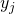 は、
は、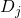 が
が 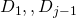 と内点を共有しないという条件下での最小の値を選ぶ。このとき、連結した円の斜めの列が形成される。パラメータ
と内点を共有しないという条件下での最小の値を選ぶ。このとき、連結した円の斜めの列が形成される。パラメータ 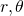 を動かすときの、葉序螺旋としての斜列係数の変化は Farey 二分木の分岐図を作る。ここでは連結成分の本数の変化に注目して報告する。
を動かすときの、葉序螺旋としての斜列係数の変化は Farey 二分木の分岐図を作る。ここでは連結成分の本数の変化に注目して報告する。
-
◎ある2次元ソリトン方程式の解とネットワーク / ○城戸 真弥 (早稲田大学数学応用数理専攻), 田中 悠太 (早稲田大学数学応用数理専攻), 渡邉 靖之 (早稲田大学数学応用数理専攻), 丸野 健一 (早稲田大学), 筧 三郎 (立教大学) [概要]
KP方程式のソリトン解のロンスキアン表示について,コード図やネットワークを用いたソリトンパターンの分類はよく知られている.KP方程式の一般化の一つであるDKP方程式のソリトン解のロンスキ型パフィアン表示について,反対称行列の標準化とそのネットワーク表示を与えることによってKP方程式に現れるネットワークが簡単に得られることを示し,DKP方程式特有な解についてそのネットワーク表示を与える.
-
◎スペクトラル特徴量スケーリングの多クラス分類問題への拡張 / ○松田 萌望 (筑波大学), 保國 惠一 (筑波大学), 今倉 暁 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
高次元データの2クラス分類問題に対する精度を改善するために、特徴量のスケールを調整するための因子(スケーリング因子)を固有値問題に基づいて計算する教師あり学習手法を近年我々は提案した。この手法を多クラス分類問題に対して拡張するため、2クラス分類毎に固有値問題を1つ解いて得られる複数のスケーリング因子を組み合わせて用いる手法を提案する。
-
◎様々な Hele-Shaw 型問題の基本解近似解法による統一的数値解法 / ○榊原 航也 (京都大学・理研), 矢崎 成俊 (明治大学) [概要]
古典的 Hele-Shaw 問題は狭い間隙を持つセル内の流体運動を記述し,フィンガリング現象を調べるための最も基本的なモデルとして,広く研究されてきた.本ポスター発表では,まずHele-Shaw 問題に対する,基本解近似解法を用いた構造保存数値解法を提唱し,その解析結果を述べる.そして,間隙が時間に依存する Hele-Shaw 問題,時間逆向き曲率流の安定化など,様々な問題に適用できることを示し,その有用性を数値実験を通して確認する.
-
◎成分濃縮ネットワークでの分離特性関数および不均一性の平衡解への影響 / ○照山 楓 (茨城大学), 三瓶 貴俊 (茨城大学), 渡邊 辰矢 (茨城大学) [概要]
複数の成分が混合した流体から標的成分を取り出すために、弱い分離を起こす受動素子を多数並べた2次元ネットワークを考える。素子の分離特性関数の影響を調べ、非単調な場合には平衡解が不安定になり得ること、素子の濃縮方向が入口濃度により逆転する場合には完全に分離できないことを示す。素子と接続部の不均一性の影響も調べ、濃度の揺らぎがパラメタの揺らぎに比例すること、接続部の欠損に対しては頑健であることを示す。
-
ベイズ推定を用いた並列数値計算ライブラリの性能予測 / ○原田 祐希 (鳥取大学), 田中 和幸 (鳥取大学), 福本 智哉 (鳥取大学), 深谷 猛 (北海道大学), 山本 有作 (電気通信大学), 星 健夫 (鳥取大学) [概要]
ハードもソフトも複雑となった今日の計算科学において、実行前の消費時間予測は重要である。特に,問題サイズやノード数についての外挿的性能予測が期待される。本研究では、並列一般化固有値計算を例として、ソースコードを元に消費時間についてルーチンごとのモデル式を構築し、実測データを元にベイズ推定を行った。予測結果は幅を持った値として得られ、外挿としての性能飽和が再現された。複数モデルを用いて、比較も行った。
-
一般アルキメデス螺旋格子による葉序的なボロノイタイリング / ○須志田 隆道 (北海道大学 電子科学研究所), 山岸 義和 (龍谷大学 理工学部) [概要]
ひまわりなどの螺旋葉序の幾何学モデルの一つとして、一般アルキメデス螺旋格子を母点集合とする平面のボロノイタイリングを考える。本講演では、一般アルキメデス螺旋格子のボロノイタイリングにおいて定義される斜列係数の分岐過程が回転角の連分数展開で記述されることを示す。さらに、斜列係数が分岐する箇所に出現する円環状のパターンを構成する多角形の形状やパラメータの分岐図について得られた結果を示す。
-
◎反復線形ソルバを用いた大規模密一般化固有値問題向けSS-RR法の性能評価 / ○矢野 貴大 (筑波大学), 二村 保徳 (筑波大学), 今倉 暁 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
大規模密行列で構成されるエルミート正定値型一般化固有値問題を大規模計算機クラスタ上で解くことを考える.
本研究では周回積分型固有値解法であるSS-RR法,およびその内部で利用する連立一次方程式ソルバとしてBlock BiCGrQ法を用いた手法を提案する.
電子状態計算で現れる問題に対して,提案手法とScaLAPACKのPZHEGVXについてXeon PhiクラスタであるOakforest-PACS上で比較を行う.
-
グレゴリー級数の剰余項の連分数表示 / 薄井 宗一 (福島大学), ○笠井 博則 (福島大学), 大浦 拓哉 (京都大学) [概要]
グレゴリー級数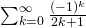 は収束の遅い級数として知られている。我々は、グレゴリー級数の値を有限和とその剰余項として表し、剰余項を連分数展開で近似することを考える。本発表では、有限和の連分数表現を2通り考え、その数値実験と相互の関係について紹介する。
は収束の遅い級数として知られている。我々は、グレゴリー級数の値を有限和とその剰余項として表し、剰余項を連分数展開で近似することを考える。本発表では、有限和の連分数表現を2通り考え、その数値実験と相互の関係について紹介する。
-
Shifted Block BiCGStab 法の近似解精度劣化の数値的原因解析 / ○倉本 亮世 (筑波大学大学院システム情報工学研究科), 多田野 寛人 (筑波大学計算科学研究センター) [概要]
複数右辺・複数シフトを持つ線形方程式の数値解法であるShifted Block BiCGStab法は行列ベクトル積を行わずにシフト方程式の近似解の更新を行うことができる.しかしながら,問題によってはシフト方程式の近似解の精度が劣化することがある.漸化式で計算する残差と真の残差の乖離がこの原因であるが,シフト方程式では偽の残差を陽的に計算しないため,残差の偽収束を改善することが難しい.本研究では,シフト方程式の近似解精度劣化の原因について,数値的に解析を行う.
-
◎CCMによる力学系ネットワーク構造の推定2 / ○井上 晟綜 (大阪府立大学工学研究科), 堀田 武彦 (大阪府立大学工学研究科) [概要]
従来、決定論的力学系における因果関係を推定する方法であるCCMでは直接的な因果性と間接的な因果性を区別することができなかった。
その問題を解決するために、時系列データに条件をつけることでCCMによる因果推定の結果がどのように変化するか調べた。
-
◎Einstein方程式の2次摂動まで考慮した数値計算 / ○福島 実紗 (早稲田大学大学院基幹理工学研究科), 土屋 拓也 (早稲田大学基幹理工学部), 米田 元 (早稲田大学基幹理工学部) [概要]
昨年度の年会の発表では、Einstein方程式の1次の線型近似で重力波の波形の数値計算を行ったが、実際の重力波の波形は2次以上の高次の非線形で与えられることが知られている。そこで、今回は2次の非線形効果まで考慮した数値計算を行った。
-
◎シフト付きCholeskyQR法を用いた一般内積空間におけるQR分解の計算 / 深谷 猛 (北海道大学), 中務 佑治 (国立情報学研究所), Kannan Ramaseshan (Arup, UK), 山本 有作 (電気通信大学), ○柳澤 優香 (早稲田大学 理工学術院総合研究所) [概要]
CholeskyQR法は高性能計算に適したQR分解の計算手法であるが,数値安定性に欠けることが知られている.近年,我々は,CholeskyQR2法およびシフト付きCholeskyQR法を提案し,CholeskyQR法に対して計算精度と数値安定性が改善されることを証明するとともに,依然として計算時間の意味でも優れていることを確認した.本発表では,CholeskyQR法に関する最新の研究成果を紹介するとともに,これらの手法を一般内積におけるQR分解に応用することを考える.アルゴリズムの計算コストや精度を理論的・実験的に他の手法と比較することで,その有用性を示す.
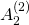 型クラスター代数の生成元について / ○野邊 厚 (千葉大学教育学部) [概要]
型クラスター代数の生成元について / ○野邊 厚 (千葉大学教育学部) [概要]
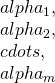 (但し、
(但し、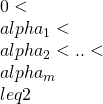 )をもつ一般のべき則(べき指数の種類
)をもつ一般のべき則(べき指数の種類